W trójkącie ABC , mamy dane : AC=4 , BC=AB-2 oraz kąt ACB =60 stopni. Oblicz GOGA: W trójkącie ABC , mamy dane : AC=4 , BC=AB−2 oraz kąt ACB =60 stopni. Oblicz sinusy kątów CAB i ABC . Prosze o rozpisanie zadania k rok po kroku !

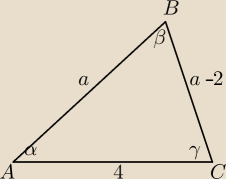
Basia: γ=60 z tw.cosinusów masz a² = 4² + (a−2)² − 2*4*(a−2)*cosγ a² = 16 + a²−4a + 4 − 8(a−2)*¹₂ a² = a² + 20 − 4a − 4(a−2) a² = a² + 20 −4a −4a + 8 0 = −8a + 28 8a = 28

	28		7
a =		=
	8		2

a−2 = ⁷₂−⁴₂ = ³₂ teraz zastosuj tw.sinusów

a		a−2		4
	=		=
sin60		sinα		sinβ

podstaw dane i wylicz sinα i sinβ

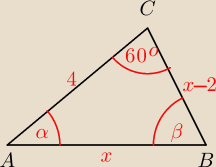
Gustlik: Wskazówka: Zastosuj oznaczenia jak na rysunku i najpierw oblicz x z tw. cosinusów: x²=4²+(x−2)²−2*4*(x−2)*cos60^o Będziesz znał długości boków AB i BC. A potem z tw. sinusów:

x		4
	=
sin60o		sinβ

oraz

x		x−2
	=
sin60o		sinα

GOGA: a dlaczego są takie oznaczenia ,że AB=x i CB =x−2, ? a gdy jest tak AB=x i BC=x+2 to wychodzi źle ?

Mila: |BC|=|CB|=x−2 z treści zadania, po oznaczeniu AB=x Jeśli dałaś x+2 to zmieniłaś długość BC.

GOGA: Jakie BC=CB=x−2 , ?

GOGA: już wiem o co chodzi wielkie dzięki

Kacyper: nudziło mi się to narysowałem sobie czołg

5-latek: No piekny