geometria analityczna - okrąg qwerty: Punkty A=(0, 4), B=(2, 0), C=(−4, 0) należą do okręgu. Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.

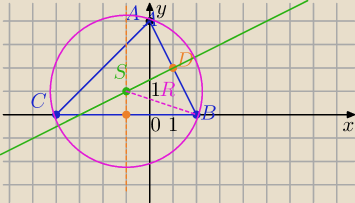
Mila: AB,BC,AC są cięciwami okręgu. środek okręgu opisanego na Δ leży na przecięciu symetralnych boków Δ Symetralna BC ma równanie: x=−1 Prosta AB: y=ax+4, 0=2*a+4, a=−2, y=−2x+4

	1
Symetralna AB: y=		x+b
	2

	0+2		4+0
D=(		,		)=(1,2) środek AB
	2		2

	1		3
2=		+b, b=
	2		2

	1		3
Symetralna AB ma równanie: y=		x+
	2		2

	1		3
Obliczamy wsp. punktu przecięcia dwóch symetralnych: x=−1, y=−		+		=1
	2		2

S=(−1,1) R=|SB|=√1²+3²=√10 Dalej dokończ

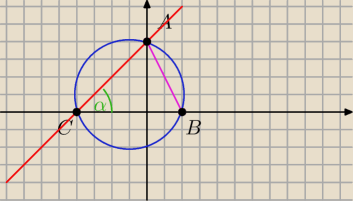Saizou : można też

	YC−YA		0−4		−4
aAC=		=		=		=1
	XC−XA		−4−0		−4

tgα=a_ac=1→α=45^o lABl=√(2−0)²+(0−4)²=√4+16=√20=2√5 i z tw. sinusów

	lABl
2R=
	sinα

	lABl
R=
	2sinα

	2√5
R=
	√2   2*   2

	2√5
R=
	√2

	2√10
R=		=√10
	2

Mila: Ładnie, Saizou.

Saizou : taki trochę szybszy sposób mi się wydaje, bo nie trzeba szukać środka okręgu ale w sumie to kwestia wprawy w rachunkach