Napisz równanie płaszczyzny przechodzącej przez punkty
iwona: hej
,
Mam problem z zadaniem..oto one:
Napisz równanie płaszczyzny przechodzącej przez punkty A(1,0,−3), B(2,2,2), C(0,0,4), a
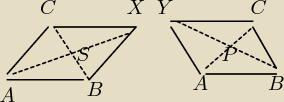
następnie znajdź wierzchołek X równoległoboku ABCX.
dziekuje za pomoc
AS:
Sposób 1
Równanie ogólne płaszczyzny: A*x + B*y + C*z + D = 0
Dzielę stronami przez D ≠ 0
| A | | B | | C | | D | |
| *x + |
| *y + |
| *z + |
| = 0 |
| D | | D | | D | | D | |
| | A | | B | | C | |
Kładąc |
| = a , |
| = b , |
| = c otrzymamy równanie postaci |
| | D | | D | | D | |
a*x + b*y + c*z + 1 = 0
a − 3*c + 1 = 0 po wstawieniu wsp. punktu A
2*a + 2*b + 2*c + 1 = 0 po wstawieniu wsp. punktu B
4*c + 1 = 0 po wstawieniu wsp. punktu C
Rozwiązując ten układ otrzymujemy
| | −7 | | 3 | | −1 | |
a = |
| b = |
| c = |
| a równanie przybierze postać |
| | 4 | | 2 | | 4 | |
| −7 | | 3 | | −1 | |
| *x + |
| *y + |
| + 1 = 0 |*(−4) |
| 4 | | 2 | | 4 | |
7*x − 6*y + z − 4 = 0
Sposób 2
Równanie wyznacznikowe płaszczyzny
| x y z 1 |
|xA yA zA 1| = 0
|xB yB zB 1|
|xC yC zC 1
|x y z 1 |
|1 0 −3 1 | = 0
|2 2 2 1|
|0 0 4 1||
|0 −3 1| | 1 −3 1| |1 0 1| |1 0 −3|
x*|2 2 1| − y*| 2 2 1| + z* |2 2 1| − |2 2 2| = 0
|0 4 1| | 0 4 1| |0 0 1| |0 0 4|
x*14 − y*12 + z*2 − 8 = 0 |:2
7*x − 6*y + z − 4 = 0
Zadanie 2
Przypadek 1
A(1,0,−3) , B(2,2,2) , C(0,0,4)
Środek odcinka BC
| | 2 + 0 | | 2 + 0 | | 2 + 4 | |
x1 = |
| = 1 , y1 = |
| = 1 , z1 = |
| = 3 |
| | 2 | | 2 | | 2 | |
S(1,1,3)
Środek odcinka AX
| 1 + x | | 0 + y | | −3 + z | |
| = 1 ⇒ x = 1 , |
| = 1 ⇒ y = 2 , |
| = 3 ⇒ z = 9 |
| 2 | | 2 | | 2 | |
X(1,2,9)
Przypadek 2
Proszę powtórzyć to samo działanie samemu.
Odp. X' (−1,−2,−1)