Obszar całkowania ograniczony równaniami okręgu w postaci x^2+y^2=y nobody: Witam, Siedzę nad prostym zadaniem, ale nie potrafię wyrysować sobie obszaru do całkowania. Zadanie jest następujące: Oblicz całkę ∬xdD, gdzie obszar D jest ograniczony krzywymi x²+y²=y; x²+y²=2y; y=x (y≥x) (obszar D zapisać we współrzędnych biegunowych). Wiem, że pierwsze dwie krzywe to równania okręgu, ale nie potrafię wyobrazić sobie, jak mogę to narysować. Używając wolframa jest bardzo łatwo, ale ja nie spotkałem się nigdy z tym zapisem, a w materiałach, które mam nie znalazłem podobnego zadania. Proszę o pomoc.

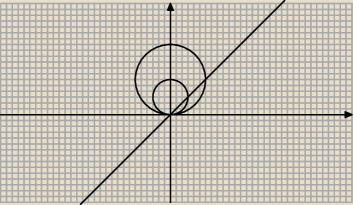
nobody: Zacząłem rozwiązywać i ... nawet wychodzi podobnie, jak w wolframie. 1. podmieniamy x i y na postacie biegunowe: x = rcos(φ), y = rsin(φ) 2. wstawiamy do podanych wzorów na krzywe a) r²cos²(φ)+r²sin²(φ)=rsin(φ) b) r²cos²(φ)+r²sin²(φ)=2*rsin(φ) z a) r = sin(φ) −> φ∊(0,2π), stąd r(min)=0, r(max)=1 z b) r = 2*sin(φ) −> φ∊(0,2π), stąd r(min)=0, r(max)=2, jest dwukrotnie większy. Oba okręgi mają początek w punkcie (0,0). prosta y=x po wyrysowaniu przecina oba okręgi. Rysunek jest czysto poglądowy, bo nie chciało mi się bawić z jednostkami.

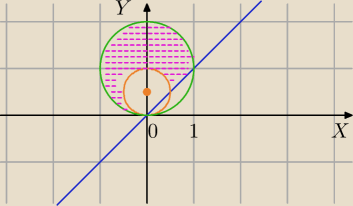
Mila: 1) x²+y²=y⇔x²+y²−y=0⇔

	1		1		1		1
x2+(y−		)2=		, S1=(0,		), r=		postać kanoniczna równania okręgu
	2		4		2		2

2) x²+y²−2y=0⇔x²+(y−1)²=1, S₂=(0,1),R=1 3)y≥x punkty powyżej prostej y=x

nobody: Dziękuję za zapis matematyczny. Zastanawia mnie, jak policzyć zakreskowane pole, jeśli policzę całkę po podstawieniu za x = rcos(φ), za granice wezmę z zewnątrz r od 0 do 2, od wewnątrz całki od 0 do 2π, to po obliczeniu całki z cos(φ) zostanie mi sin(φ), po podstawieniu granic wyjdzie 0. Plan wymyśliłem taki, żeby policzyć pola ograniczone poszczególnymi okręgami, odjąć małe pole z dużego a następnie doliczyć brakujący fragment dla każdego z okręgów, dodać mniejszy wycinek i odjąć większy, żeby nie odjąć za dużo, ale po co w takim razie podana wstępnie w zadaniu całka ?

PW: Ale masz policzyć nie pole D, ale pewną całkę na tym obszarze.

Mila: Podziel obszar na 3 części. Całkę rozbij na 3 całki.

nobody: PW: Przepraszam, ale nie bardzo rozumiem. Czy jest dostępny gdzieś (z szybkim dostępem, bo jutro egzamin) materiał z obliczania takich całek oprócz tego, co nagrał e−trapez ?

Mila: http://wmii.uwm.edu.pl/~kost/wyklad_M_2_13.pdf

nobody: Nie potrafię zamienić dla tej całki granic całkowania dla obszaru D. r zmienia się oczywiście w granicach 0−2, ale nie mam żadnego pomysłu na drugą całkę. Chyba, że przekształcenie na współrzędne biegunowe są drugą częścią zadania, a nie poradą (nie mam dostępu do oryginału, żeby sprawdzić). W takim przypadku mogę podzielić duży okrąg na te 3 części, które sugerowałaś. Od 0 do π, od π do ³₂π i ⁷₄π do 2π (tego ostatniego nie jestem pewien). Pozostaje jeszcze kwestia funkcji ...

Trivial: >>>r zmienia się oczywiście w granicach 0−2 z tym oczywiście to bym się zastanowił.

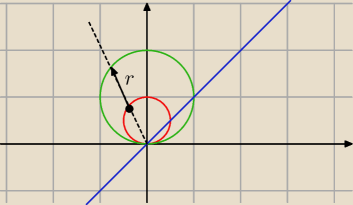
Trivial: Zapisujemy równania we współrzędnych biegunowych 1) r² = rsinφ → r = sinφ 2) r² = 2rsinφ → r = 2sinφ Skąd już widać, że

	⎧	sinφ ≤ r ≤ 2sinφ
G:	⎩	π/4 ≤ φ ≤ π

∬_D x dD = ∬_G rcosφ*rdrdφ = ∫_π/4^π cosφdφ ∫_sinφ^2sinφ r²dr =

	7		7		7		7
= ∫π/4π		sin3φcosφdφ =		∫1/√20 u3du = −		= −
	3		3		3*4*4		27

Trivial:

	7		7
Ehm, nie wiem dlaczego napisało mi się −		. Poprawna odpowiedź to oczywiście −		.
	27		48

nobody: Pomyłka w widzeniu Po prostu siedzenie długo nad nauką nie zawsze daje w 100% pozytywne efekty. Promień, a nie średnica dużego okręgu to r=1, czyli granica 0−1. Tym razem nie oczywiście Prawdę mówiąc zgłupiałem już przy tym zadaniu.Jeśli chodzi o przedział 0 do π, to liczyłbym go patrząc względem osi x (tak, jak jest teraz), natomiast pozostałe obszary obróciłbym tak, żeby były normalne względem osi y. Czy jest to poprawne rozumowanie (oczywiście po dobraniu odpowiednich przedziałów) ? Jeśli tak, to nie jestem pewien czy dobrze rozumiem kolejną rzecz. Całka będzie wynosiła tyle, ile suma tych trzech wcześniej obliczonych ?

Trivial: Granica na r nie jest ani od 0 do 2, a nie od 0 do 1. W tym zadaniu r zmienia się od sinφ do 2sinφ, co zresztą widać bardzo dobrze na obrazku. Przecięcie prostą wychodzącą ze środka dobrze obrazuje jak się zmienia r (strzałka na obrazku!). Co do φ to również nie jest to od 0

	π
do π, tylko od		do π (ponownie odsyłam do rysunku).
	4

Całki można oczywiście sumować, czyli jeżeli podzielisz sobie obszar D na kilka obszarów D₁,D₂,...,D_n parami rozłącznych (∀ k≠m D_k∩D_m = ∅) to mamy wtedy: ∬_D f(x,y)dxdy = ∬_D1 f(x,y)dxdy + ∬_D2 f(x,y)dxdy + ... + ∬_Dn f(x,y)dxdy

nobody: Dziękuję za pomoc. Mój błąd polegał na tym, że (nie wiem jakim cudem) patrzyłem na rysunek tak, jakby duży okrąg miał środek w punkcie (0,0), stąd pewnie te wszystkie pomyłki i trudności. Wstyd −,−