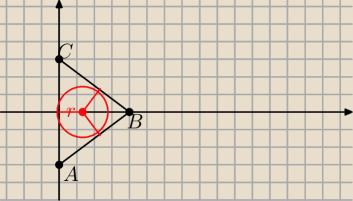
 zauważ, że AB i CB są symetryczne względem osi OX
czyli oś OX jest dwusieczną kąta ABC
zatem S, który leży na dwusiecznej kąta ABC musi leżeć na OX
S(x;0) x>0 ale to jest równocześnie promień tego okręgu czyli
S(r;0) r>0
odległość S od AC = r
teraz potrzeba i wystarcza aby odległość S od pr.AB i pr.BC= r
1. piszesz równanie prostej AB
2. zapisujesz odległość S od pr.AB
3. przyrównujesz do r; rozwiązujesz równanie
4. masz współrzedne S; masz promień; piszesz równanie okręgu
zauważ, że AB i CB są symetryczne względem osi OX
czyli oś OX jest dwusieczną kąta ABC
zatem S, który leży na dwusiecznej kąta ABC musi leżeć na OX
S(x;0) x>0 ale to jest równocześnie promień tego okręgu czyli
S(r;0) r>0
odległość S od AC = r
teraz potrzeba i wystarcza aby odległość S od pr.AB i pr.BC= r
1. piszesz równanie prostej AB
2. zapisujesz odległość S od pr.AB
3. przyrównujesz do r; rozwiązujesz równanie
4. masz współrzedne S; masz promień; piszesz równanie okręgu
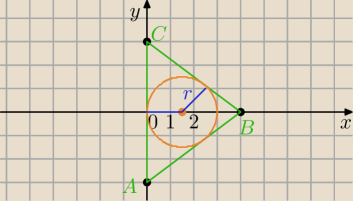 Środek okręgu wpisanego w trójkąt leży w punkcie przecięcia dwusiecznych kątów wewnętrznych,
jedną z dwusiecznych jest oś Ox
S=(x,0)
S jest jednakowo odległy od boków ΔABC
AC: x=0
Środek okręgu wpisanego w trójkąt leży w punkcie przecięcia dwusiecznych kątów wewnętrznych,
jedną z dwusiecznych jest oś Ox
S=(x,0)
S jest jednakowo odległy od boków ΔABC
AC: x=0
| −3 | ||
BC: y=ax+3 i 0=4*a+3⇔y= | x+3⇔3x+4y−12=0 | |
| 4 |
| |3*x+4*0−12| | ||
d= | odległość punktu S=(x,0) od prostej BC | |
| √32+42 |
| |3x−12| | ||
d= | i x>0 | |
| 5 |
| |3x−12| | |
=x i x>0 | |
| 5 |
| 3 | 3 | |||
x=−6∉D lub x= | i r= | |||
| 2 | 2 |
| 3 | 9 | |||
(x− | )2+y2= | |||
| 2 | 4 |
| 1 | ||
W tym zadaniu łatwo jest obliczyć pole trójkąta: P = | *6*4 = 12 | |
| 2 |
| L | 2P | 2*12 | 3 | |||||
Pole trójkąta to także P = | *r ⇒ r = | ⇒ r = | = | |||||
| 2 | L | 16 | 2 |