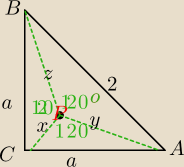 Przeczytaj o punkcie Torricellego. (jak radzi kolega Vax)
Rozwiąż np. tak.
PΔABC=1
1) porównaj sumę pól małych Δ z polem ΔABC⇒obliczysz sumę (xy+xz+yz)
2) W każdym "małym" Δ zastosuj twierdzenie cosinusów⇒otrzymasz układ równań.
3)Rozwiąż układ równań.
Przeczytaj o punkcie Torricellego. (jak radzi kolega Vax)
Rozwiąż np. tak.
PΔABC=1
1) porównaj sumę pól małych Δ z polem ΔABC⇒obliczysz sumę (xy+xz+yz)
2) W każdym "małym" Δ zastosuj twierdzenie cosinusów⇒otrzymasz układ równań.
3)Rozwiąż układ równań.
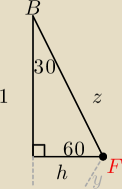 x, y, z − odcinki od wierzchołka do punktu Fermata (jak na ilustracji Mili)
W trójkącie prostokątnym ΔACB (gdzie przeciwprostokątna to odcinek |AB|, jak na ilustracji
Mili)
punkt F (Fermata) dzieli ΔACB na ΔCFA, ΔBFC i ΔAFB.
ΔAFB jest trójkątem równoramiennym, o ramieniach z oraz y (patrz ilustracja Mili), dzięki
czemu
z = y
Wysokość h trójkąta ΔAFB przecina trójkąt na dwa trójkąty prostokątne o kątach 60°, 90°
oraz 180°−60°−90°, z czego wynika że mamy doczynienia z trójkątem 60° 90° 30°.
https://www.matemaks.pl/trojkat-prostokatny-30-60-90.html
hΔAFB = 1 / √3
z = 2h = 2 / √3
y = 2 / √3
x+hΔAFB = hΔACB
hΔACB = 1
x = 1 − 1 / √3
x+y+z = 1−1 / √3+ 2 /√3+2 / √3
x+y+z = 1+4 / √3−1 / √3
x+y+z = 1+3 / √3
3 / √3 = 3√3 / (√3*√3) = 3√3 / 3 = √3
x+y+z = 1+√3
x, y, z − odcinki od wierzchołka do punktu Fermata (jak na ilustracji Mili)
W trójkącie prostokątnym ΔACB (gdzie przeciwprostokątna to odcinek |AB|, jak na ilustracji
Mili)
punkt F (Fermata) dzieli ΔACB na ΔCFA, ΔBFC i ΔAFB.
ΔAFB jest trójkątem równoramiennym, o ramieniach z oraz y (patrz ilustracja Mili), dzięki
czemu
z = y
Wysokość h trójkąta ΔAFB przecina trójkąt na dwa trójkąty prostokątne o kątach 60°, 90°
oraz 180°−60°−90°, z czego wynika że mamy doczynienia z trójkątem 60° 90° 30°.
https://www.matemaks.pl/trojkat-prostokatny-30-60-90.html
hΔAFB = 1 / √3
z = 2h = 2 / √3
y = 2 / √3
x+hΔAFB = hΔACB
hΔACB = 1
x = 1 − 1 / √3
x+y+z = 1−1 / √3+ 2 /√3+2 / √3
x+y+z = 1+4 / √3−1 / √3
x+y+z = 1+3 / √3
3 / √3 = 3√3 / (√3*√3) = 3√3 / 3 = √3
x+y+z = 1+√3
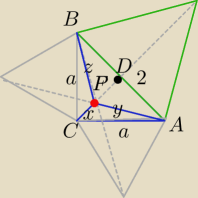 Dobrze .
Popraw zapisy;
Ułamki piszemy za pomocą dużej litery U
U{licznik} {mianownik} bez tej spacji między klamrami.
Dobrze .
Popraw zapisy;
Ułamki piszemy za pomocą dużej litery U
U{licznik} {mianownik} bez tej spacji między klamrami.
 z = y
z = y
| 1 | ||
hΔAFB = | ||
| √3 |
| 2 | ||
z = 2h = | ||
| √3 |
| 2 | ||
y = | ||
| √3 |
| 1 | ||
x = 1 − | ||
| √3 |
| 1 | 2 | 2 | ||||
x+y+z = 1 − | + | + | ||||
| √3 | √3 | √3 |
| 4 | 1 | |||
x+y+z = 1 + | − | |||
| √3 | √3 |
| 3 | ||
x+y+z = 1 + | ||
| √3 |
| 3 | 3*√3 | 3√3 | |||
= | = | = √3 | |||
| √3 | √3*√3 | 3 |

