 TREŚĆ:
boki trojkata ABC sa rowne a,b,c. Oblicz dlugosc srodkowej poprowadzonej z wierzcholka A do
boku a.
zrobilem to tak ze oznaczylem srodkowa jako odcinek x. nastepnie dla kata zaznaczonego na
rysunku po prawej wyznaczylem wartosc (180−sinα) a wiec dla kata u gory wystarczy dac wartosc
180 stopni
nastepnie porownalem pola obu trojkatow na ktore dzieli srodkowa i wyszly ze sa one rowne.
skoro srodkowa dzieli bok a na dwie rowne czesci oraz jest ona bokiem wspolnym dla obu
trojkatow (jak zreszta i bok a ) to wynika z tego fakt ze boki calego trojkata czyli "b" i "c"
musza tez byc rowne.
a wiec wywnioskowalem ze jest to trojkat rownoramienny i srodkowa opuszczona na bok "a" dzieli
go na polowy i jest zarazem wysokoscia tego trojkata
nastepnie zrobilem pitagorasa x2 + 1/4x2 = b2
po odpowiednim przeksztalceniu doszedlem do obliczenia x.
PROSZE MI POWIEDZIEC CZY TO ZADANIE JEST ZROBIONE PRZEZEMNIE DOBRZE. POZDRAWIAM
.
TREŚĆ:
boki trojkata ABC sa rowne a,b,c. Oblicz dlugosc srodkowej poprowadzonej z wierzcholka A do
boku a.
zrobilem to tak ze oznaczylem srodkowa jako odcinek x. nastepnie dla kata zaznaczonego na
rysunku po prawej wyznaczylem wartosc (180−sinα) a wiec dla kata u gory wystarczy dac wartosc
180 stopni
nastepnie porownalem pola obu trojkatow na ktore dzieli srodkowa i wyszly ze sa one rowne.
skoro srodkowa dzieli bok a na dwie rowne czesci oraz jest ona bokiem wspolnym dla obu
trojkatow (jak zreszta i bok a ) to wynika z tego fakt ze boki calego trojkata czyli "b" i "c"
musza tez byc rowne.
a wiec wywnioskowalem ze jest to trojkat rownoramienny i srodkowa opuszczona na bok "a" dzieli
go na polowy i jest zarazem wysokoscia tego trojkata
nastepnie zrobilem pitagorasa x2 + 1/4x2 = b2
po odpowiednim przeksztalceniu doszedlem do obliczenia x.
PROSZE MI POWIEDZIEC CZY TO ZADANIE JEST ZROBIONE PRZEZEMNIE DOBRZE. POZDRAWIAM
.

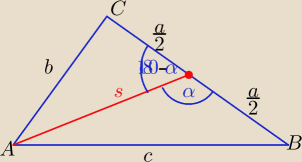 Z tw. cosinusów
Z tw. cosinusów
| a2 | a | |||
c2= s2+ | −2*s* | *cosα cos(180o−α)= −cosα | ||
| 4 | 2 |
| a2 | a | |||
i b2= s2+ | +2*s* | *cosα | ||
| 4 | 2 |
| a2 | ||
c2+b2=2s2+ | /*2 | |
| 2 |
| 1 | ||
s= | √2c2+2b2−a2 | |
| 2 |