Zadanie z wartością bezwzględną
Bogdan: Rozwiąż równanie:
lx+1l−lxl+3lx−1l−2lx−2l=lx+2l
Wyznaczam przedziały wyliczam niewiadomą i wychodzi mi jedno rozwiązanie x=−2 a w odpowiedziach
są przedziały potrafi mi ktoś wytłumaczyć na jaki inny sposób rozwiązać te zadanie by było
zgodne z odpowiedzią?
26 wrz 19:35
matyk: strasznie dużo tych przedziałów

pokaż jak robisz.
26 wrz 19:43
bogdan: A czy jest mozliwosc by wynikiem równania była nierówność? Bo możliwe ze jest błąd w odpowiedzi
26 wrz 20:42
ZKS:
Jest taka możliwość.
26 wrz 20:44
26 wrz 20:45
Mila:
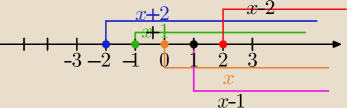
Przedziały na osi.
lx+1l−lxl+3lx−1l−2lx−2l=lx+2l
1) x<−2 wszystkie wyrażenia ujemne:
−x−1−(−x)+3(−x+1)−2(−x+2)=−x−2⇔
−x−1+x−3x+3+2x−4=−x−2⇔
−x−2=−x−2 prawda niezależnie od wartości x.⇔
0=0 ⇔każda liczba z przedziału (−
∞, −2) spełnia równanie
x∊(−∞,−2)
2) x∊<−2,−1)
|x+2|=x+2 dla pozostałych zmieniamy znaki
−x−1+x−3x+3+2x−4=x+2⇔−x−2=x+2
−4=2x ⇔
x=−2∊<−2,−1)
3)x∊<−1,0)
|x+2|=x+2 i |x+1|=x+1
x+1+x−3x+3+2x−4=x+2⇔x=x+2
0=2 sprzeczność , brak rozwiązań w tym przedziale
4)x∊<0,1)
x+1−x+3(−x+1)−2(−x+2)=(x+2)
x+1−x−3x+3+2x−4=x+2
−x=x+2
−2x=2
x=−1∉<0,1)
5) x∊<1,2)
x+1−x+3x−3+2x−4=x+2
5x−6=x+3
4x=9
6) x≥2
x+1−x+3x−3−2x+4=x+2
x+2=x+2 prawda niezależnie od wartości x
x∊<2,∞)
odp.
x∊(−∞,−2) lub
x∊<2,∞) lub x=−2
mam nadzieję, że nie ma literówek, źle sie pisze taki długi tekst.
26 wrz 20:53
PW:
|x+1|+3|x−1| = |x+2|+|x|+2|x−2|
Wystarczy wziąć takie x, dla których wszystkie wyrażenia "między kreseczkami" są nieujemne (z
muszą być dostatecznie duże), a równanie przyjmie postać
x+1+3(x−1) = x+2+x+2(x−2)
4x−2 = 4x−2,
jest to równanie tożsamościowe, spełnione przez wszystkie x z dziedziny (rozwiązaniem tego
równania są wszystkie x∊<2,∞).
Podobnie gdy x są dostatecznie małe − mniejsze niż −2 − równanie też będzie tożsamościowe
−(x+1)−3(x−1) = −(x+2)−x−2(x−2).
To tylko uwaga na temat "w odpowiedzi są przedziały", a nie kompletne rozwiązanie.
26 wrz 21:37
Bogdan: Zapomniałem o tym 0=0 to każda z liczb spełnia równanie. Dzięki za pomoc!
26 wrz 21:42
PW: Mila, jak zwykle (prawie) byłem leniwy (nie odświeżyłem długo, bo bym nic nie pisał widząc
Twoje rozwiązanie), ale nie znalazłem tylko jednego rozwiązania. Rzeczywiście koszmarne
"rozbijanie na przedziały"

26 wrz 21:43
Mila: 
26 wrz 21:44
 pokaż jak robisz.
pokaż jak robisz.
 Przedziały na osi.
lx+1l−lxl+3lx−1l−2lx−2l=lx+2l
1) x<−2 wszystkie wyrażenia ujemne:
−x−1−(−x)+3(−x+1)−2(−x+2)=−x−2⇔
−x−1+x−3x+3+2x−4=−x−2⇔
−x−2=−x−2 prawda niezależnie od wartości x.⇔
0=0 ⇔każda liczba z przedziału (−∞, −2) spełnia równanie
x∊(−∞,−2)
2) x∊<−2,−1)
|x+2|=x+2 dla pozostałych zmieniamy znaki
−x−1+x−3x+3+2x−4=x+2⇔−x−2=x+2
−4=2x ⇔ x=−2∊<−2,−1)
3)x∊<−1,0)
|x+2|=x+2 i |x+1|=x+1
x+1+x−3x+3+2x−4=x+2⇔x=x+2
0=2 sprzeczność , brak rozwiązań w tym przedziale
4)x∊<0,1)
x+1−x+3(−x+1)−2(−x+2)=(x+2)
x+1−x−3x+3+2x−4=x+2
−x=x+2
−2x=2
x=−1∉<0,1)
5) x∊<1,2)
x+1−x+3x−3+2x−4=x+2
5x−6=x+3
4x=9
Przedziały na osi.
lx+1l−lxl+3lx−1l−2lx−2l=lx+2l
1) x<−2 wszystkie wyrażenia ujemne:
−x−1−(−x)+3(−x+1)−2(−x+2)=−x−2⇔
−x−1+x−3x+3+2x−4=−x−2⇔
−x−2=−x−2 prawda niezależnie od wartości x.⇔
0=0 ⇔każda liczba z przedziału (−∞, −2) spełnia równanie
x∊(−∞,−2)
2) x∊<−2,−1)
|x+2|=x+2 dla pozostałych zmieniamy znaki
−x−1+x−3x+3+2x−4=x+2⇔−x−2=x+2
−4=2x ⇔ x=−2∊<−2,−1)
3)x∊<−1,0)
|x+2|=x+2 i |x+1|=x+1
x+1+x−3x+3+2x−4=x+2⇔x=x+2
0=2 sprzeczność , brak rozwiązań w tym przedziale
4)x∊<0,1)
x+1−x+3(−x+1)−2(−x+2)=(x+2)
x+1−x−3x+3+2x−4=x+2
−x=x+2
−2x=2
x=−1∉<0,1)
5) x∊<1,2)
x+1−x+3x−3+2x−4=x+2
5x−6=x+3
4x=9

