Z wierzchołka ostrosłupa prawidłowego... Dejwid: Z wierzchołka ostrosłupa prawidłowego trójkątnego poprowadzono wysokości dwóch ścian bocznych. Miara kąta między tymi wysokościami jest równa 60 stopni, a krawędź boczna tego ostrosłupa ma długość 4{2} . Oblicz objętość i pole całkowite ostrosłupa. Proszę o wytłumaczenie krok po kroku.

Dejwid: 4√2

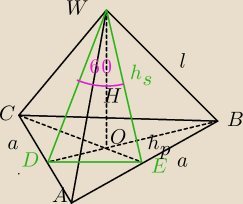
dero2005: |EW| = |DW| = h_s l = 4√2

	a
ponieważ podstawa jest trójkątem równobocznym kat DAE = 60o, |AE| = |AD| =		to odcinek
	2

	a
|ED| też równy jest		. ponieważ kąt DWE jest równy 60o a |EW| = |DW| to trójkat DWE
	2

	a
jest równoboczny i hs =
	2

Rozpatrzmy trójkąt EBW i tw Pitagorasa (^a₂)² + (^a₂)² = l²

a2
	= 32
2

a² = 64 a = 8 h_s = 4

	2
|OB| =		hp
	3

	a√3
a hp =		= 4√3
	2

	2		8
to		hp =		√3
	3		3

z Pitagorasa H² = l² − (²₃h_p)² H² = 32 − ⁶⁴₃ = ³²₃

	4
H =		√6
	3

	a2√3
Pp =		=
	4

	3
Pb =		a*hs =
	2

P_c = P_b + P_b =

	Pp*H
V =		=
	3

mądrala : tylko idioci się uczą...