POMOCY Koksu: Wyznacz wartosc nsjmniejsza i wartosc najwiesza funkcji f w podanym przedziale a) f(X)=2x²−4x+3,<0;3>

	4
Xw=		=1 ∊<0;3>
	4

Yw=f(1)=2−4+3=1 f(0)= f(3)= wartosc najmniejsza wartosc najwieksza B) f(x)=−3x²−6x−2,<1;2>

	−6
Xw=		=−1 ∉ <1;2>
	−6

f(1)= f(2)= wnajm wnajw

	1
C)f(x)=		x2+2x+1,<−6;2>
	4

wartosc najm wartosc najw D)

	2
f(x)=		x2−x,<−3,0>
	3

wartosc najm wartosc najw

Koksu:

Mila: 1) f(X)=2x²−4x+3,<0;3> parabola skierowana do góry skoro x_w∊<0,3>, to wartość najmniejsza y_min=y_w=1 Wartość najwieksza − f(3)=2*9−4*3+3=9 jeśli nie wiesz ktry argument wybrać, to liczysz dla 0 i 3 a potem wybierasz większą [f(0)=3] 2)f(x)=−3x²−6x−2,<1;2> parabola skierowana w dół

	6
xw=		=−1∉ <1,2>
	−6

Liczysz wartości: dla 1 i 2 f(1)= −3−6−2=−11 wartość największa w przedziale <1;2> f(2)=−2*4−6*2−2= −8−12−2=−22 wartość najmniejsza w przedziale <1;2>

	1
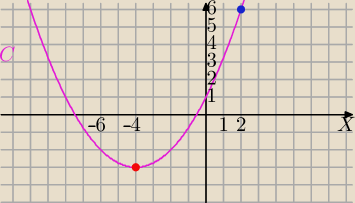
3) f(x)=		x2+2x+1 , x∊<−6,2) parabola skierowana do góry
	4

	−2
xw=		=−4∊<−6,2>
	0,5

	1
yw=		*16+2*(−4)+1=−3 to wartość najmniejsza ymin=yw=−3
	4

liczysz na końcach przedziału

	1
f(−6)=		*36+2*(−6)+1=9−12+1=−2
	4

	1
f(2)=		*4+2*2+1=6 wartość największa w przedziale <−6;2>
	4

Do tego masz rysunek Ostatnie teraz rozwiąż sam.