okrąg lena: dla jakich wart . parametru m okręgi mają jeden punkt wspólny ? jak dokończyć ? a) x²+y²−4x−2y+1=0 x²+y²+x−y+−m= b)x² + y²−4x+2y+4=0 x²+y²+2x−6y+10 − ^m₄ w a wyszło mi s₁(2,1) r₁ = 2 zaś S₂(−3,2) r₂ √m²−2m+9 |S₁S₂|= √26 i co dalej ? jak policzyć . w b S(2, −1 ) r₁=1 ,a S₂ (−1,3) r₂ = ^√m₂ |S₁S₂|= 5 . nie wiem co dalej robić może źle policzyłam

Basia: ad.a S₁ i r₁ dobrze; S₂ i r₂ źle −2a = 1 a = −u{1}[2} −2b = −1 b = ¹₂ S₂ = (−¹₂; ¹₂) r₂² = ¹₄+¹₄−(−m) = m+¹₂

	√26
S2S1 = √(2+12)2+(1−12)2 = √(25/4)+(1/4) = √26/4 =
	2

1. zewnętrznie styczne

	√26
r1+r2 =
	2

	√26
2 + √m+12 =
	2

	√26
√m+(1/2) =		− 2
	2

	√26−4
√m+(1/2) =		/()2 (można; obie strony nieujemne)
	2

	1		(√26−4)2
m+		=
	2		4

	(√26−4)2		1
m =		−
	4		2

	26 − 8√26 + 16 − 2		40 − 8√26
m =		=		= 10 − 2√26
	4		4

2. wewnętrznie styczne

	√26
|r1−r2| =
	2

	26
(r1−r2)2 =
	4

	26
(2 − √m+(1/2))2 =
	4

	1		26
4 − 4√m+(1/2) + m+		=
	2		4

16		2		26
	+		−		+m = 4√m+(1/2)
4		4		4

	8
m −		= 4√m+(1/2)
	4

m − 2 = 4√m+(1/2) (m−2)² = m+¹₂ m² − 4m + 4 = m+¹₂ /*2 2m² − 8m + 8 = 2m + 1 2m² − 10m + 7 = 0 Δ = 100 − 56 = 44 √Δ = √44 = 2√11

	10−2√11		5−√11
m1 =		=
	4		2

	5+√11
m2 =
	2

nie pomyliłaś się w przepisywaniu równania okręgu drugiego ? załozyłam, że to jest x²+y²+x−y−m = 0 może jest jakoś inaczej, bo koszmarne te rachunki

	√m
w (2) od razu musisz założyć, że m>0, bo inaczej r2 =
	2

albo nie istnieje albo jest = 0 i dokończyć tak jak w (1) rachunki będą tutaj proste

Gustlik: Wyznacz współrzędne środka i promień obu okręgów ze wzorów: x²+y²+Ax+By+C=o

	A
a=−
	2

	B
b=−
	2

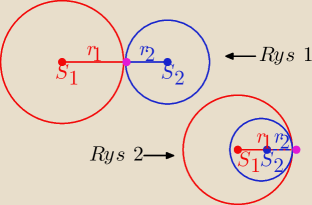
r=√a²+b²−C, gdy a²+b²−C>0 Okregi maja 1 punkt wspólny ⇔ są styczne zewnętrznie (rys. 1) lub wewnętrznie (rys. 2)⇔ |S₁S₂|=r₁+r₂ (rys. 1) lub |S₁S₂|=|r₁−r₂| (rys. 2). Wskazówka: oblicz współrzedne wektora S₁S₂^→, a potem zastosuj wzór na długość wektora: a^→=√a_x²+a_y² i masz odległość środków i porównaj ją z sumą i różnicą promieni, otrzymasz warunek na styczność.