Wyznacz w zależności od wartości parametru m, liczbę rozwiązań równania Lukas: I3x−1/x−2I=m

Rafał28:

Rafał28:

Rafał28:

3x − 1		3(x − 2) + 5		5
	=		=		+ 3
x − 2		x − 2		x − 2

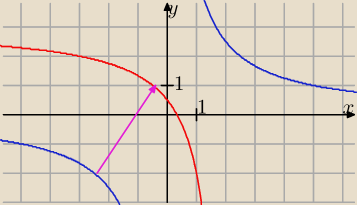
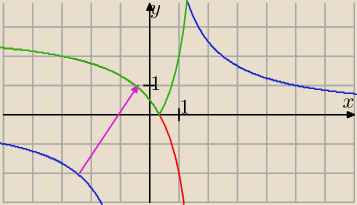
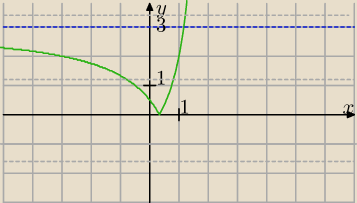
Rysujemy wykres funkcji g(x) = ⁵_x, przesuwamy równolegle o wektor u^→ = [2, 3] otrzymując wykres funkcji h(x) = ⁵ _{x − 2} + 3 i odbijamy część wykresu h(x) o wartościach ujemnych względem osi OX uzyskując wykres funkcji f(x) = |(3x−1)/(x−2)| Z drugiej strony funkcja r(x) = m, m∊R może być dowolną funkcją stałą. Odpowiedź. Dla m∊(−∞, 0) brak rozwiązań (brak punktów wspólnych funkcji f(x), r(x)) Dla m∊{0}∪<3, +∞) jedno rozwiązanie (jeden punkt wspólny funkcji f(x), r(x)) Dla m∊(0, 3) dwa rozwiązania (dwa punkty wspólne funkcji f(x), r(x))

Lukas: dzięki za pomoc, ale mam jedno pytanie. Czy drugiej hiperboli nie bierze się pod uwagę w rozwiązaniu zadania?

Rafał28: Nie bierze, ona ma być tylko pomocna w rysowaniu funkcji f(x)

Lukas: ok, zrozumiałem