Wykładnicza z parametrem - wykres TheeMI: Hej. Potrzebuję małej pomocy w zadaniu z funkcji wykładniczej z parametrem. Zbadaj liczbę rozwiązań równania w zależności od wartości parametru m (m∊R) 2^|x−2|+x = m² Jeżeli chodzi o część pierwszą to wszystko jest dobrze. Zrobiłem to na przypadki.

⎧	22x−2 dla x≥2
⎩	22 dla x<2

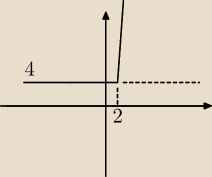
Teraz rysunek. Może nie jest to dobrze przedstawione, ale zawsze jakiś podgląd ; ). Jak przedstawić liczbę rozwiązań ?. Jakby było =m to nie ma problemu, ale m² ?

Basia: m² ∊<0;4) nie masz rozwiązań m²≥0 (zawsze) m²<4 ⇔ m∊(−2;2) czyli dla m∊(−2;2) nie ma rozwiązania m² = 4 nieskończenie wiele rozwiązań m²=4 ⇔ m= −2 lub m=2 czyli dla m= ±2 masz nieskończenie wiele rozwiązań m²>4 masz jedno rozwiązanie m²>4 ⇔ m∊(−∞; −2)∪(2;+∞) czyli dla m∊(−∞; −2)∪(2;+∞) masz jedno rozwiązanie

TheeMI: Dzięki. Teraz zagłębię się w zrozumieniu.

TheeMI: Prostsze niż myślałem. Chyba z każdym zadaniem tak jest : ).

Basia: