 tak więc
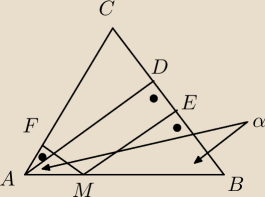
ΔAFM ≈ ΔEMB ≈ ΔADB z cechy kkk (mają wspólny kąt α oraz wszystkie trzy są prostokatne)
Dla jasności ∡FAM na rysunku jest kątem α.
Zatem :
tak więc
ΔAFM ≈ ΔEMB ≈ ΔADB z cechy kkk (mają wspólny kąt α oraz wszystkie trzy są prostokatne)
Dla jasności ∡FAM na rysunku jest kątem α.
Zatem :
| |AM| | |MB| | |AB| | |||
= | = | ||||
| |FM| | |EM| | |AD| |
| |FM| * |AB| | ||
|AM|(|EM| + |FM| ) = |FM| * |AB| , ale przecież |AM| = | i dostaje : | |
| |AD| |
| |EM| + |FM| | |
= 1 ⇒ |EM| + |FM| = |AD| | |
| |AD| |