Punkty wspólne okręgu i prostej
adam: Okrąg o środku w punkcie O(−1,2) i promieniu √10 ma dwa punkty wspólne z prostą AB gdy:
a) A (−3,−2) B(1,−1)
b) A (−2,−5) B(2,2)
c) A (0,5) B(3,4)
d) A (2,1) B(4,7)
Jak w ogóle zacząć to zadanie? Nie mam w ogóle pomysłu żadnego od czego zacząć.
24 wrz 22:45
Technik:
A prosta AB jaki ma wzór ?
24 wrz 22:47
adam: No właśnie nie jest podane dlatego nie wiem jak to ruszyć. Myślę aby w każdym podpunkcie
wyznaczyć równanie prostej ab, potem odliczyć odległość prostej od środka okręgu i gdy
odległość środka okręgu od prostej będzie mniejsza od promienia to będą dwa punkty wspólne,
ale to wydaje się sporo roboty. może jakiś łatwiejszy sposób jest.
24 wrz 22:51
Lorak: Też tylko taki sposób przychodzi mi do głowy.
Trochę liczenia niestety będzie.
24 wrz 22:57
Mila:
równanie okręgu:
(x+1)
2+(y−2)
2=(
√10)
2⇔
(x+1)
2+(y−2)
2=10
wypadałoby napisać równania prostych i badać odległość punktu S od prostej,
jeżeli d<
√10, to prosta ma dwa punkty wspólne z okręgiem.
To dużo pracy>
Spróbujemy inaczej:
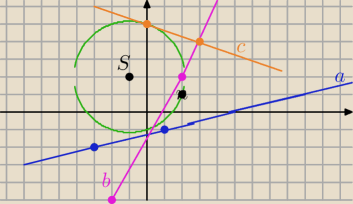
Teraz rysuję okrąg i proste
a) nie
b) Tak
c)nie
d)nie
Możesz teraz napisać równanie prostej b i rachunkiem sprawdzić.
24 wrz 23:04
 równanie okręgu:
(x+1)2+(y−2)2=(√10)2⇔
(x+1)2+(y−2)2=10
wypadałoby napisać równania prostych i badać odległość punktu S od prostej,
jeżeli d<√10, to prosta ma dwa punkty wspólne z okręgiem.
To dużo pracy>
Spróbujemy inaczej:
Teraz rysuję okrąg i proste
a) nie
b) Tak
c)nie
d)nie
Możesz teraz napisać równanie prostej b i rachunkiem sprawdzić.
równanie okręgu:
(x+1)2+(y−2)2=(√10)2⇔
(x+1)2+(y−2)2=10
wypadałoby napisać równania prostych i badać odległość punktu S od prostej,
jeżeli d<√10, to prosta ma dwa punkty wspólne z okręgiem.
To dużo pracy>
Spróbujemy inaczej:
Teraz rysuję okrąg i proste
a) nie
b) Tak
c)nie
d)nie
Możesz teraz napisać równanie prostej b i rachunkiem sprawdzić.