Wykresy funkcji y=|f(x)| mattme: Dana funkcja f(x)=|x−3|−2. Dla jakich wartości parametru k równanie |f(x)|=k + 1 ma : a) dwa rozwiązania różnych znaków b) cztery rozwiązania dodatnie ?

Eta: 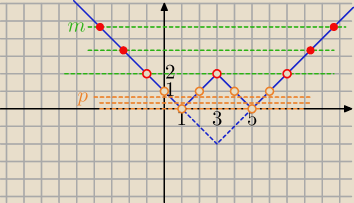_____ |f(x)| 2 rozwiązania różnych znaków dla k+1 >2 4 rozwiązania dodatnie dla 0<k+1<1

ZKS: No to jeszcze sposób algebraiczny. ||x − 3| − 2| = k + 1 (zał. k ≥ −1) Sprawdźmy co mamy dla k = −1 ||x − 3| − 2| = 0 |x − 3| = 2 x = 5 ∨ x = 1 dostajemy dwa rozwiązania dodatnie ale nie o to nam chodzi więc k = −1 nie spełnia warunków zadania |x − 3| = k + 3 ∨ |x − 3| = 1 − k dla k = 1 mamy |x − 3| = 4 ∨ |x − 3| = 0 x = 7 ∨ x = −1 ∨ x = 3 mamy trzy rozwiązania więc również nie spełnia warunków zadania dla k > 1 x = k + 6 ∨ x = −k rozwiązanie x = k + 6 jest dodatnie więc x = −k musi być ujemne k > 0 ∧ k > 1 ⇒ k ∊ (1 ; ∞) mamy dwa rozwiązania różnych znaków. Teraz rozpatrujemy kiedy będziemy mieli cztery rozwiązania dodatnie ||x − 3| − 2| = k + 1 ∧ k ≥ −1 |x − 3| = k + 3 ∨ |x − 3| = 1 − k 1 − k > 0 ⇒ k < 1 x = k + 6 ∨ x = −k ∨ x = 4 − k ∨ x = k + 2 k + 6 > 0 ∧ −k > 0 ∧ 4 − k > 0 ∧ k + 2 > 0 ⇒ k ∊ (−2 ; 0) mamy cztery rozwiązania dodatnie.

ZKS: Oczywiście na samym końcu nie uwzględniłem początkowego założenia k > −1 dla k = −1 jak pokazywałem na początku mamy dwa rozwiązania dodatnie k ∊ (−2 ; 0) ∧ k > −1 ⇒ k ∊ (−1 ; 0).

Eta: