rozwiaz rownanie Madzik: rozwiaz równanie |x| + |x+5|=2x +5 Jak to przedstawić graficznie? Dalej już chyba powinnam sb poradzic

Kostek: 1⁰(−∞,−5) −x−x−5=2x+5 −4x=10 4x=−10 x=−2,5∉(−∞,−2,5) 2⁰ <−5,0) −x+x+5=2x+5 −2x=0 2x=0 x=0∉<−5,0) 3⁰ <0,∞) x+x+5=2x=5 0=0 x∊<0,∞)

Mila: 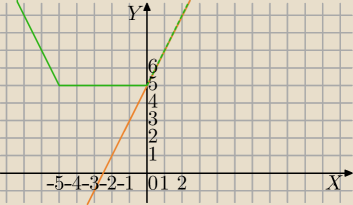f(x)=|x|+|x+5| 1)x<−5 f(x)=−x−x−5⇔f(x)=−2x−5 2)x∊<−5,0) f(x)=−x+x+5=5 funkcja stała 3) x≥0 f(x)=x+x+5⇔f(x)=2x+5 g(x)=2x+5 |x|+|x+5|=2x+5 x∊<0,∞) nieskończenie wiele rozwiązan.

PW: Przychodzi mi na myśl "leniwe" rozwiązanie. Wiadomo, że rozwiązań wystarczy szukać dla takich x, dla których prawa strona jest liczbą nieujemną (bo lewa jest nieujemna). Dla takich x mamy do czynienia z równaniem |x|+|x+5|=|2x+5| |x|+|x+5|=|x+(x+5)|, x∊<0,∞) Wiadomo, że dla dowolnych a, b spełniona jest nierówność |a|+|b| ≥ |a+b|, przy czym równość ma miejsce wtedy i tylko wtedy, gdy a•b≥0. W rozpatrywanym przedziale <0,∞) oba składniki są nieujemne, a więc równość jest spełniona dla wszystkich x∊<0,∞).