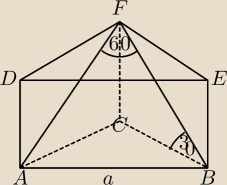
stereometria xd: Podstawą graniastosłupa prostego jest trójkąt równoramienny, którego podstawa ma długość a. przekątna FB ściany bocznej tworzy z krawędzią BC kąt 30, a kąt między przekątnymi FB i FA

	a3√2
wynosi 60. Wykaż, że objętość tego graniastosłupa jest równa
	8

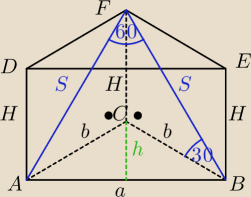dero2005: dane :a trójkąt ABF jest równoboczy(kąt 60^o) więc S = a rozpatrujemy trójkąt BCF

H		H		1
	=		= sin30o =
S		a		2

	a
H =
	2

b		b		√3
	=		= cos30o =
S		a		2

	a√3
b =
	2

liczymy wysokość podstawy h

	a√2
h = √b2 − (a2)2 = √3a24 − a24 =
	2

liczymy pole podstawy

	a*h		a2√2
Pp =		=
	2		4

liczymy objętość

	a2√2		a		a3√2
V = Pp*H =		*		=
	4		2		8

cnd