Drugie miejsce zerowe funkcji Imposible: Niech x1 bedzie jednym z miejsc zerowych funkcji kwadratowej, ktorej wierzcholek znajduje sie w punkcie W. Wyznacz (o ile istnieje) drugie miejsce zerowe tej funkcji gdy: b) x1=0, W=(1,4) c) x1=3 1:3, W=(1:2, −6) d) x1=16 √2, W=(−3, −11 II) Wyjaśnienie: 1:3 − jedna trzecia, np. 3 1:3 − trzy i jedna trzecia II − ''pi'' , np. −11 II Prosze o pomoc! Ważne na jutro Nie radze sobie z tym. Prosze o rozwiazanie i krotkie wytlumaczenie.

Imposible: Prosze o pomoc

Imposible: Błagam pomozcie potrzebuje na jutro

Imposible: pomocy

Imposible: :(

Imposible: :(

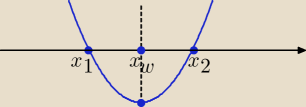
Bogdan:

	x1 + x2
xw =		⇒ x2 = 2xw − x1
	2

Imposible: a my robilismy podpunkt a na lekcji tak: y=a(x−0)² 0=a(−2−0)²+3 4a+3=0 4a=−3 /:4 a=−3:4 ( − trzy czwarte) y=ax²+bx+c y=−3:4x²+3 delta=b²−4ac delta=0²−4(−3:4).3 delta= 12:4 .3 delta=−9 no i do tego nie bylo drugiego miejsca zerowego. a niech mi ktos tym sposobem wytlumaczy b, c, d. Prosze

Imposible: pomocy

Imposible: RATUJCIE!

Imposible: przy b) delta wyszla mi = 65 a dale liczylam: x2= − b+delta/(kreska ulamkowa) 2a x2= 1+√65/−8 i nie wiem co dalej

Imposible: pomocy

Imposible: pomocy

Basia: Bogdan wskazał Ci najprostszy możliwy sposób rozwiązania zastosuj go; możesz chyba rozwiązać w sposób prostszy niż na lekcji wprawdzie nauczyciel może Cię zapytać skąd taki wzór

	x1+x2
xw =
	2

ale to łatwo uzasadnić

x1+x2		−b−√Δ   −b+√Δ   + 2a   2a
	=		=
2		2

−b−√Δ−b+√Δ   2a		−2b   2a		−b   a		−b
	=		=		=		= xw
2		2		2		2a

zastosuj to i masz rozwiązanie w jednej linijce

Imposible: a dlaczego pod x1+x2 jest 2?

Basia: czy Ty widziałaś kiedyś ułamek ?

Imposible: ?

Imposible: no tak ale dlaczego przez 2

Basia: bo jak podzielę przez 10 to nie dostanę x_w

Imposible: ?

Imposible: ja sie w tym pogubilam. dzieki za dobre checi ale ja tego nie zrobie

Imposible:

Bogdan:

	x1 + x2
xw =
	2

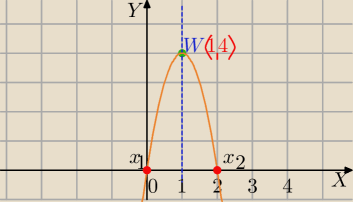
Mila: b) x₁=0, W=(1,4) Oś symetrii paraboli przechodzi przez wierzchołek paraboli x₂=2 jest odbiciem symetrycznym podanego miejsca zerowego względem prostej x=1 1 jest w środku między x₁ i x₂ Możesz policzyć tak:

	0+x2
1=
	2

2=x₂

Mila:

	3 1		1
c) x1=		, W=(		, −6)
	3		2

x1+x2		1
	=		/*2⇔
2		2

x₁+x₂=1

31
	+x2=1
3

	1
x2=1−10
	3

	1
x2=−9
	3

d) x₁=16 √2, W=(−3, −11 π)

x1+x2
	=−3 /*2
2

x₁+x₂=−6 16√2+x₂=−6 x₂=−6−16√2