Równiania liniowe Mati: Mam problem z kilkoma zadaniami. Nie wiem w jaki sposób je rozwiązywać. 1.Wyznacz wartości parametru m , dla których zbiór rozwiązań nierówności 4m−x≤x+3 a) jest przedziałem <5.+∞) b) zawiera się w przedziale <1,+∞). 2.Wyznacz wartość parametru m , dla których zbiór rozwiązań nierówności mx+5>0 a) jest zbiorem liczb rzeczywistych b) jest zbiorem pustym. 3. Wyznacz wartości parametru m ,dla których dziedziną funkcji f(x)=√2−m−x jest przedział <1,+∞) Byłbym wdzięczny jakby ktoś pokazał w jaki sposób robić zadania tego typu, nie chce tylko rozwiązania.

Basia: (1) 4m − x ≤ x + 3 −x − x ≤ −4m + 3 −2x ≤ −4m + 3 /: (−2)

	4m−3
x ≥
	2

	4m−3
x∊<		;+∞)
	2

czyli w (a) musi być

4m−3
	= 5
2

wylicz sobie m w (b) musi być

	4m−3
1 ≤
	2

rozwiąż i zobacz jaki warunek spełnia m jeżeli czegoś nie rozumiesz pytaj

Mati: @Basia, nie było mnie akurat na tych lekcjach a w klasie robili to w ten sposób że przyrównywali nierówność do 0 a za x wstawiali to co było określone w poleceniu. A czemu później przyrównujesz to do 5? A co odnośnie 3 Dzięki bardzo za normalne wytłumaczenie

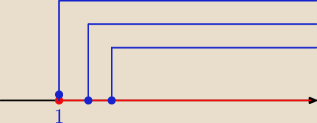
Basia: wyszło mi rozwiązanie

	4m−3
x∊ <		; +∞)
	2

	4m−3
i ma być <		; +∞) = <5;+∞)
	2

	4m−3
no to przecież żeby tak było musi być		= 5
	2

	4m−3
a żeby było <		; +∞) ⊂ <1;+∞) to musi być
	2

4m−3
	≥ 1
2

	4m−3
niebieski to ten <		; +∞) (różne możliwości)
	2

najpierw (1); do następnych przejdziemy jak to zrozumiesz

Mati:

	4m−3
A i czemu w tym 2. 1≤		tak przyrównałaś?
	2

Basia: co ma do tego x=0 ? wprawdzie różne kretyństwa już przy równaniach z parametrem widziałam, ale takiego jak dotąd jeszcze nie

Basia: no bo <10;+∞) ⊂<1;+∞) <9;+∞)⊂<1;+∞) <1,000001; +∞) ⊂ <1;+∞) <1;+∞) ⊂ <1;+∞) ale <0,999999;+∞); <0;+∞) itd już nie czyli lewy koniec tego naszego musi być ≥ 1

Basia: poza tym to nie jest (2); to jest (1b)

Mati: Czyli jeśli jest przedziałem to po wyznaczeniu x musimy przyrównać to do przedziału aby było to zgodne. A w przypadku aby się zawierały w tym przedziale musi być tak samo jak w przedziale.

Mati: Wiem , później się zorientowałem. Teraz już rozumiem te zadanie 1.

Basia: to teraz (2) mx+5 > 0 mx > −5 i tu musimy rozważyć dwa przypadki nie możemy bezkarnie dzielić przez m, bo m może = 0 mamy więc: 1. m=0 wtedy 0*x > −5 0 > − 5 to jest prawdą dla każdego x∊R czyli dla m=0 zbiorem rozwiązań jest R dla m≠0 chcemy podzielić, ale to jest nierówność, która inaczej się zachowa gdy m<0, a inaczej gdy m>0; więc znów musimy rozważyć dwa przypadki 2. m>0 mx>−5 /:m

	−5
x >
	m

	−5
x∊(		;+∞)
	m

nie ma takiej możliwości, żeby to był zbiór R, ale nie ma też takiej żeby to był zbiór ∅ 3. m<0

	−5
x <
	m

	−5
x∊ (−∞;		)
	m

nie ma takiej możliwości, żeby to był zbiór R, ale nie ma też takiej żeby to był zbiór ∅ ostatecznie: (a) dla m=0 (b) nigdy

Mati: A jak np. mam (m+2)(m−3)x+m>0

	−m		−m
To w opcji z pustym wychodzi x<		, i x>		, jak z tego wyjść?
	(m+2)(m−3)		(m+2)(m−3)

Mati: A mógłbym otrzymać nr.gg do Ciebie?

Basia: musisz rozważyć różne przypadki: 1. m = −2 masz 0*(−5)*x −2 > 0 −2 >0 sprzeczność dla m=−2 nie ma rozwiązania (inaczej zb.rozw. = ∅) 2. m = 3 masz 5*0*x + 3 > 0 3>0 tożsamość dla m=3 zb.rozw.=R 3. (m+2)(m−3)>0 ⇔ m∊(−∞;−2)∪(3;+∞) masz

	−m
x >
	(m+2)(m−3)

	−m
zb.rozw. = (		; +∞)
	(m+2)(m−3)

4. (m+2)(m−3)<0 ⇔ m∊(−2;3)

	−m
x <
	(m+2)(m−3)

	−m
zb.rozw. = (−∞;		)
	(m+2)(m−3)

Imposible: Pomózcie mi blagam

Basia: nie używam gg, nie działało mi na Ubuntu jak należy i się poddałam; może znowu kiedyś spróbuję, ale raczej nie dzisiaj; czasem udzielam korepetycji przez Skype'a, ale rzadko i ..........................

Mati: Nie no spoko, ale i tak nie daję mi to jednoznacznego rozwiązania, w opdowiedziach jest ze liczba −2, czyli ta która de fakto nie pasuje do pierwszego czy nie lepiej od razu zakładać taki przypadek niż liczyć tyle? A czy na 3. jest też jeden sposób?

Imposible: pomocy

Basia: nie napisałeś mi Mati treści zadania więc Ci napisałam całe kompletne rozwiązanie nierówności jeżeli było pytanie dla jakiego m zb.rozw. = ∅ to i tak trzeba wszystko policzyć bo skąd wiadomo, czy jeszcze dla jakiegoś innego m tak nie będzie ?

Mati: Dlatego ja osobiście się zdziwiłem kiedy po prostu podstawiali to,dziwne też jest że podręcznik zakłada tylko tę opcję, skoro tak jak mówisz może ich być więcej. I ponowie pytanie: Jak z 3?

Basia: 2−m−x ≥ 0 (bo jest pod pierwiastkiem) x ≤ 2−m tu nie trzeba rozważać żadnych przypadków, bo nie dzielimy przez wyrażenie, w którym jest parametr zb.rozw. = (−∞; 2−m> nie ma takiego m dla którego ten przedział mógłby stać się przedziałem <1;+∞)

Basia: może pytanie było inaczej sformułowane; na przykład tak: jaki będzie zbiór rozwiązań dla m = −2 wtedy oczywiście wystarczy sprawdzić dla m= −2, czyli podstawić

Mati: NIe właśnie, nie, Dlatego pisałem o to, Bo nie problem napisać idąc tym przykładem że wybieramy tą drugą opcję. Ale niech pojawi się co innego i za przeproszeniem d*pa. A chcialbym to weidzieć. Dzięki wielkie za pomoc

lol: αβγΩΔΔΔΔ∑≠≈←∫⊂∊♥