okręgi , położenie alexxaan: 1)okrąg o środku S (−1,2) styczny do okręgu x² + y² + 6x − 8y+16=0 może mieć promień równy ? w odp jest że 3−2√2 . policzyłam punkt S₂ i promień r₂ następnie długość S₁S₂ ale co dalej żeby to wykazać że będzie taka odp . 2)okrąg o środku S (−5,5) i promieniu r ma dwa punkty wspólne z okręgiem x²+y²=8 tu odp wynosi r=8 ale jak to policzyć ? żeby miały 2 punkty musi być że r₁−r₂ < | S₁S₂| < r₁+r₂ .. 3) jeśli okrąg ma długość 20 pi ma jeden punkt wspólny z okręgiem x² + y²=25, to jego środkiem może być punkt ? odp /(4,3) wyjaśni ktoś , pomoże obliczyć ?

Basia: jeżeli okręgi są styczne zewnętrznie to S₁S₂ = r₁+r₂ a jeżeli wewnętrznie to S₁S₂ = |r₁−r₂|

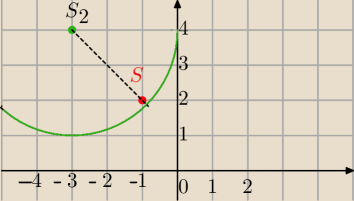
Mila: 1) S (−1,2) styczny do okręgu x² + y² + 6x − 8y+16=0 Postać kanoniczna : (x+3)²−9+(y−4)²−16+16=0 (x+3)²+(y−4)²=3² S₂=(−3,4) , R=3 S∊ wnętrza koła, okręgi mogą być styczne wewnętrzenie. |SS₂|=√(−3+1)²+(4−2)²=√4+4=2√2 2√2<3 r=R−|SS₂|=3−2√2