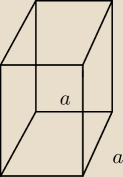
Oblicz objętość tego graniastosłupa. wajdzik: Podstawą graniastosłupa prostego jest romb o bokach długości a i kącie rozwartym o mierze

	2π
		. Przekątne dwóch ścian bocznych wychodzących z wierzchołka kąta rozwartego dolnej
	3

	π
podstawy tworzą kąt		. Oblicz objętość tego graniastosłupa.
	4

Mam problem ze stereometrią, w ogóle nie wiem jak się brać na początku za takie zadania. Może ktoś pomóc?

dero2005:

	d*f
Pp = a2*sin260o =
	2

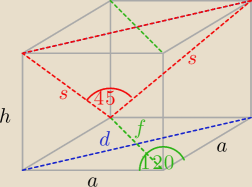
ponieważ kąt ostry wnosi 60^o f = a obliczamy d z wzoru cosinusów obliczmy s z wzoru Pitagorasa obliczmy h V = P_p*h =

wajdzik: dzięki, już analizuje.

wajdzik: d obliczę z tw. Pitagorasa

	1
a2+(		a)2=d2
	2

	1
d2=		a2+a2
	4

	5
d2=		a2
	4

	a√5
d=
	2

wajdzik: Nie, nie obliczę d z tw. Pitagorasa, już zmieniam..

wajdzik:

	d*f
a2sin260=
	2

2a²*sin²60=d*a

	2a2sin260
d=		=2a*sin260
	a

teraz się zgadza?

wajdzik:

dero2005:

	√3
Pp = a2sin60o = a2*
	2

	d*f
Pp =
	2

ale f = a bo kąt ostry ma 60^o porównujemy wzory i wstawiamy f = a

	√3		d*a
a2		=
	2		2

d = a√3 teraz zajmiemy się trójkątem czerwonym i obliczamy s ze wzoru cosinusów d² = 2s² − 2s²cos45^o

	√2
3a2 = 2s2(1 −		)
	2

	2−√2
3a2 = 2s2(		)
	2

	3
s2 =		a2(2+√2)
	2

obliczamy wesokość h z pitagorasa h² = s² − a² = 3a²(2+√2) − a² = a²(5−3√2) h = a√5−3√2 liczymy objętość

	a3√3
V = Pp*h =		√5−3√2
	2

czy tak może być