;0' Justyna: Zdarzenia A i B spełniają warunki: P(A)=1/3, P(A|B)=1/5, P(A|B`)=1/2. Oblicz P(B). Oraz odpowiedz na pytanie czy zdarzenia A i B się wykluczają?

sushi_ gg6397228: rozpisz z definicji prawdopodobienstwa warunkowe

Justyna:

	P(A∩B)
P(A|B)=
	P(B)

	P(A∩B`)
P(A|B`)=
	P(B`)

sushi_ gg6397228: rozpisz A∩B' (kolor zielony) P(B')= 1− P(B) masz 2 rownaini z dwoma niewiadomymi− przyjmij sobie x,y za odpowiednie prawdopodobienstwa, aby lepiej sie liczyło

Gustlik:

	1
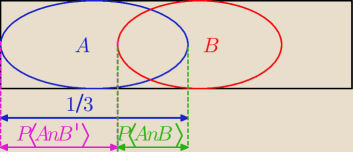
Z rysunku widać, że P(A∩B)+P(A∩B')=P(A)=		(1)
	3

Ze wzorów na prawdopodobienstwo warunkowe (podanych przez Justynę) mamy:

	1
P(A∩B)=P(A|B)*P(B)=		P(B) (2)
	5

	1
P(A∩B')=P(A|B')*P(B')=P(A|B')*[1−P(B)]=		*[1−P(B)] (3)
	2

Podstawiając (2) i (3) do (1) mamy:

1		1		1
	P(B)+		*[1−P(B)]=
5		2		3

Niech P(B)=x, żeby się łatwiej pisało

1		1		1
	x+		*[1−x]=		/*30
5		2		3

6x+15[1−x]=10 6x+15−15x=10 −9x=−5 /:(−9)

	5
Odp: P(B)=x=
	9

Gustlik: Żeby zdarzenia sie wykluczały, to P(A∩B)=0 U Ciebie

	1		5		1
P(A∩B)=P(A|B)*P(B)=		*		=		≠0, czyli zdarzenia się nie wykluczają, bo mają część
	5		9		9

wspólna.

Justyna: WIELKIE DZIĘKI

Gustlik: