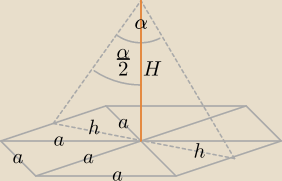
ostrosłup sześciokątny karmelka: mam takie zadanie: Wysokość ostrosłupa prawidłowego sześciokątnego wynosi H, a kąt między

	3
ścianami bocznymi wynosi		π (oznaczony jako α). Obliczyć objętość ostrosłupa i tg kąta
	4

(oznaczony jako β) nachylenia ściany bocznej do podstawy. Teoretycznie po części mam zrobione to zadanie, tylko problem jest taki że i objętość i tg kąta (β) mam uzależnione od długości krawędzi postawy (oznaczyłam jako a). Może mi ktoś teraz pomóc jak uzależnić tą długość krawędzi podstawy a od wysokości ostrosłupa i/lub kąta α między sąsiednimi ścianami bocznymi?

karmelka: pomóżcie

karmelka: jakieś pomysły

Bogdan:

	1		h		α		α
h =		a√3,		= tg		⇒ h = H tg
	2		H		2		2

1		α		2√3
	a√3 = H tg		/*		⇒ a = ...
2		2		3

	1		1
Objętość V =		* 6 *		a2√3 * H
	3		4

Bogdan:

	H
tgβ =
	h

Eta: Dla Bogdana .......... a nawet

Bogdan: Dla Ety