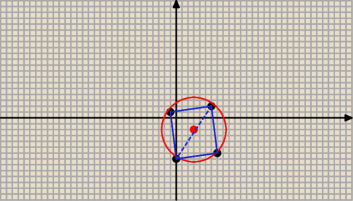
Wierzchołki kwadratu Monika: Punkt A(6,2) jest wierzchołkiem kwadratu wpisanego w okrąg x² +y² −6x+4y−12 = 0. Wyznacz współrzędne pozostałych wierzchołków kwadratu. Podaj równanie okręgu wpisanego w ten kwadrat.

Janek191: x² + y² − 6 x + 4y − 12 = 0 ( x − 3)² − 9 + ( y + 2)² − 4 − 12 = 0 ( x − 3)² + ( y + 2)² = 25 S = ( 3; − 2) r² = 25 ⇒ r = 5 A = ( 6; 2) − wierzchołek kwadratu ABCD Prosta AS : y = ax + b 2 = 6a + b − 2 = 3a + b −−−−−−−−−−−−−−− odejmujemy stronami 4 = 3a

	4
a =
	3

	4
b = 2 − 6a = 2 − 6*		= 2 − 8 = − 6
	3

	4
y =		x − 6
	3

−−−−−−−−−−−−−−−− Ta prosta przecina dany okrąg w punkcie C oraz S jest środkiem odcinka AC, czyli

	6 + x		2 +y
3 =		− 2 =
	2		2

6 + x = 6 2 + y = − 4 x = 0 y = − 6 C = ( 0; − 6) =========

	4
Prosta prostopadła do prostej o równaniu y =		x − 6 przecina okrag
	3

w punktach B i D.

4
	*a2 = − 1
3

	3
a2 = −
	4

	3
y = −		x + b2 S = ( 3; − 2)
	4

więc

	3
− 2 = −		*3 + b2
	4

	9
− 2 = −		+ b2
	4

	9		8		1
b2 =		−		=
	4		4		4

	3		1
y = −		x +
	4		4

==================== ( x − 3)² + ( y + 2)² = 25

	3		1
y = −		x +
	4		4

−−−−−−−−−−−−−

	3		9
( x − 3)2 + ( −		x +		)2 = 25
	4		4

	9		27		81
x2 − 6 x + 9 +		x2 −		x +		= 25 / *16
	16		8		16

16 x² − 96 x + 144 + 9 x² − 54 x + 81 = 400 25 x² − 150 x − 175 = 0 / : 25 x² − 6 x − 7 = 0 Δ = 36 − 4*1*( −7) = 36 + 28 = 64

	6 − 8		6 + 8
x =		= − 1 ∨ x =		= 7
	2		2

więc

	3		1		3		1
y = −		*(−1) +		= 1 ∨ y = −		*7 +		= − 5
	4		4		4		4

Odp. B = ( − 1; 1) , C = ( 0; − 6) , D = (7; − 5) ====================================

Janek191: cd. A = ( 6; 2), B = ( − 1; 1) I AB I ² = ( − 1 −6)² + ( 1 − 2)² = 49 + 1 = 50 = 25*2 więc I AB I = 5 √2 2 r₁ = I AB I = 5 √2 r₁ = 2,5 √2 r₁² = 6,25*2 = 12,5 Równanie okręgu wpisanego w kwadrat ( x − 3)² + ( y + 2)² = 12,5 =======================

Gustlik: Janek191, Współrzędne środka okręgu i promień można wyznaczyć dużo prościej − ze wzorów: x²+y²+Ax+By+C=0

	A
a=−
	2

	B
b=−
	2

r=√a²+b²−C, gdy a²+b²−C>0 Ty rozwiązałeś najtrudniejszą metodą ze wszystkich możliwych. x² + y² − 6 x + 4y − 12 = 0

	−6
a=−		=3
	2

	4
b=−		=−2
	2

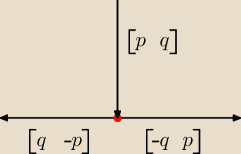
r=√3²+(−2)²−(−12)=√9+4+12=√25=5 S=(3, −2), r=5 Równanie prostej też wyznaczyłeś najbardziej skomplikowaną metodą ze wszystkich możliwych, to można rozwiązać wektorami, jeżeli wektor AB→=[w_x, w_y], to współczynnik kierunkowy prostej,

	wy
na której on leży wyraża się prostym wzorem: a=		:
	wx

A = (6; 2) S=(3, −2) AS^→=[3−6, −2−2]=[−3, −4]

	−4		4
a=		=
	−3		3

	4
y=		x+b
	3

	4
2=		*6+b
	3

2=8+b b=−6

	4
y=		x−6
	3

Metody dobre, ale pojechałeś z Warszawy do Łodzi przez Nowy Jork, a można o wiele szybciej i łatwiej. c.d. A = ( 6; 2) B = ( − 1; 1) |AB| tez prościej wektorami: AB^→=[−1−6, 1−2]=[−7, −1] |AB|=√(−7)²+(−1)²=√49+1=√50=5√2

Bogdan: Szkic rozwiązania z zastosowaniem wektorów

	6		−4
A = (6, 2), S = (		,		) = (3, −2) − środek okręgu i środek odcinka AC
	2		2

C = (x_C, y_C) x_C + 6 = 2*3 ⇒ x_C = 0, y_C + 2 = 2*(−2) ⇒ y_C = −6, C = (0, −6) → → → AS = [−3, −4], SB = [−4, 3], SD = [4, −3], B = (3 − 4, −2 + 3) = (−1, 1), D = (3 + 4, −2 − 3) = (7, −5)

Eta: i po bólu

Bogdan: