Trygonometria-Obliczanie obwodu trapezu
Melitap: Podstawy trapezu mają długości 10 i 4, a jego ramiona tworzą z dłuższą podstawą kąty 45 stopni
i 60 stopni. Oblicz obwód tego trapezu.
22 wrz 11:30
5-latek: Zrobie CI frytki a TY w tym czasie zrobisz rysunek i zobaczysz trojkaty szczegolne 45,45 90, i
drugi 30,60,90.
22 wrz 11:35
Melitap: Przepraszam. To zadanie wydaje mi się trudne
22 wrz 11:51
Melitap: Czy mogę prosić o dalsze wskazówki?
22 wrz 11:53
Janek191:
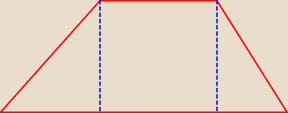
a = x + b + y = 10
b = 4
h − wysokość trapezu
c, d − długości ramion trapezu
α = 45
o ⇒ h = x ⇒ c
2 = x
2 + x
2 = 2 x
2 ⇒ c =
√2 x
| | √3 | | √3 | | 2x | |
β = 60o ⇒ h = d |
| ⇒ x = d |
| ⇒ 2x = d √3⇒ d = |
| |
| | 2 | | 2 | | √3 | |
y
2 + h
2 = d
2
| | 4 x2 | | 4x2 | | 3 x2 | | x2 | |
y2 = d2 − x2 = |
| − x2 = |
| − |
| = |
| |
| | 3 | | 3 | | 3 | | 3 | |
| | √3 | |
a = x + b + y = x + 4 + |
| x = 10 |
| | 3 | |
3x +
√3 x = 18
| | 18 | | 18*( 3 − √3) | |
( 3 + √3) x = 18 ⇒ x = |
| = |
| = |
| | 3 + √3 | | ( 3 + √3)*(3 − √3) | |
= 3*( 3 −
√3)
więc
c = 3*( 3 −
√3)*
√2 = 9
√2 − 3
√6
| | 2*3*( 3 − √3) | |
d = |
| = 6 √3 − 6 |
| | √3 | |
Obwód
L = a + b + c + d = 10 + 4 + 9
√2 − 3
√6 + 6
√3 − 6 = 8 + 9
√2 + 6
√3 − 3
√6
===============================================================
II sposób: ( funkcje trygonometryczne )
h = x
| | h | | x | | x | | √3 | |
|
| = |
| = tg 60o = √3 ⇒ x = √3 y ⇒ y = |
| = |
| x |
| | y | | y | | √3 | | 3 | |
więc
| | √3 | |
x + b + y = x + 4 + |
| x = 10 |
| | 3 | |
3 x +
√3 x = 18
( 3 +
√3) x = 18
| | 18 | |
x = |
| = 3*( 3 − √3) |
| | 3 + √3 | |
| | √3 | |
y = |
| * 3*( 3 − √3) = 3√3 − 3 |
| | 3 | |
c = x *
√2 = 3*( 3 −
√3)*
√2 = 9
√2 − 3
√6
y = d*0,5
2y = d
d = 2*(3
√3 − 3) = 6
√3 − 6
Obwód
L = a + b +c + d = 10 + 4 + 9
√2 − 3
√6 + 6
√3 − 6 = 8 + 9
√2 + 6
√3 − 3
√6
================================================================
22 wrz 16:41
Janek191:
a = x + b + y = 10
b = 4
h − wysokość trapezu
c, d − długości ramion trapezu
α = 45
o ⇒ h = x ⇒ c
2 = x
2 + x
2 = 2 x
2 ⇒ c =
√2 x
| | √3 | | √3 | | 2x | |
β = 60o ⇒ h = d |
| ⇒ x = d |
| ⇒ 2x = d √3⇒ d = |
| |
| | 2 | | 2 | | √3 | |
y
2 + h
2 = d
2
| | 4 x2 | | 4x2 | | 3 x2 | | x2 | |
y2 = d2 − x2 = |
| − x2 = |
| − |
| = |
| |
| | 3 | | 3 | | 3 | | 3 | |
| | √3 | |
a = x + b + y = x + 4 + |
| x = 10 |
| | 3 | |
3x +
√3 x = 18
| | 18 | | 18*( 3 − √3) | |
( 3 + √3) x = 18 ⇒ x = |
| = |
| = |
| | 3 + √3 | | ( 3 + √3)*(3 − √3) | |
= 3*( 3 −
√3)
więc
c = 3*( 3 −
√3)*
√2 = 9
√2 − 3
√6
| | 2*3*( 3 − √3) | |
d = |
| = 6 √3 − 6 |
| | √3 | |
Obwód
L = a + b + c + d = 10 + 4 + 9
√2 − 3
√6 + 6
√3 − 6 = 8 + 9
√2 + 6
√3 − 3
√6
===============================================================
II sposób: ( funkcje trygonometryczne )
h = x
| | h | | x | | x | | √3 | |
|
| = |
| = tg 60o = √3 ⇒ x = √3 y ⇒ y = |
| = |
| x |
| | y | | y | | √3 | | 3 | |
więc
| | √3 | |
x + b + y = x + 4 + |
| x = 10 |
| | 3 | |
3 x +
√3 x = 18
( 3 +
√3) x = 18
| | 18 | |
x = |
| = 3*( 3 − √3) |
| | 3 + √3 | |
| | √3 | |
y = |
| * 3*( 3 − √3) = 3√3 − 3 |
| | 3 | |
c = x *
√2 = 3*( 3 −
√3)*
√2 = 9
√2 − 3
√6
y = d*0,5
2y = d
d = 2*(3
√3 − 3) = 6
√3 − 6
Obwód
L = a + b +c + d = 10 + 4 + 9
√2 − 3
√6 + 6
√3 − 6 = 8 + 9
√2 + 6
√3 − 3
√6
================================================================
22 wrz 16:42