wykres funkcji. Matma. : sporządz wykres funkcji wykładniczej i omów jej własnosci y=4^x+3 −1 hmm, nie wiem jakie wartości wybrać by sporzadzić tabelkę,by wyszły małe liczby ....

use:

	1
1, 0 ,
	2

5-latek: y=4^x+2 Rysujesz wykres funkcji y=4^x a potem przesuwasz go o wektor [0 2] A jakie wartosci . Normalne .

	1
np . x=−2 to y=4−2+2=		+2= policz
	42

	1
x=−1 to y=4−1+2=		+2=
	4

x=0 to y=4⁰+2=1+2= policz x=1 to y= licz i podstawiaj sobie inne x_sy i licz y_ki

Matma. : po podstawieniu w miejsce x do wzoru funckji liczb 1,0,0,5 −liczby wychodzą duże... a jeżeli funkcja określona jest wzorem y=4x+3 −1 , to wydaje mi się,że należy przesunąc wykres funkcji o 3 jednostki w lewo i jedną w dół.

Matma. : y=4^x+3 −1

Bogdan: Czy wzór jest taki: y = 4^x+3 − 1 ? Wykładnik zapisujemy w klamrach {x+3}

5-latek: A jak przy takim zapisie ja tu napisales /as TY bys odczytal/a ta funkcje jak to ja bym napisal? czy ja jestem jasnowidz Jackowski jak ma byc? Przeciez mozez sobie przyjac na osi OX jedna kratke jako 1jednostke a na osi oY jedna czy dwie kratki jako np 10 jednostek . i rysowac wykres Nikt nie powiedzial ze na obu osiach musi byc tak samo. Tylko trzeba to wyraznie napisac na dole wykresu lub zaznaczyc obok osi OX i OY

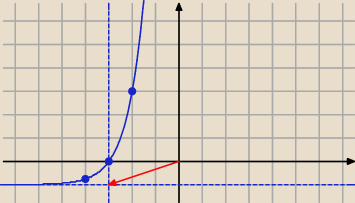
Bogdan: Szybkie szkicowanie wykresu: Jeśli y = 4^x+3 − 1, to rysujemy na układzie współrzędnych pomocnicze linie: y=−1 i x=−3 Mamy nowy "układ współrzędnych", stary układ został przesunięty o wektor [−3, −1]. Na tym "nowym układzie współrzędnych" zaznaczamy kilka punktów wykresu y = 4^x

	1
dla x = −1 ⇒ y =		, dla x = 0 ⇒ y = 1, dla x = 1 ⇒ y = 4.
	4

Łączymy zgrabnie punkty linią tworząc dla początkowego układu współrzędnych wykres y = 4^x+3 − 1

Bogdan: Oczekuję od Ciebie Matma jakiegoś słowa, np. "zrozumiałem, dziękuje" albo "dalej nie kumam"

Matma. : Bogdan − dziękuję za pomoc w tym zadaniu, rozjaśniło mi się trochę...

Matma. : ale nie wiem jakim cudem wyszły takie liczby .. jeżeli x przyjmiemy −1 , to y= 1/4 może ja coś źle podstawiam do wzoru i źle liczę

Matma. : równanie poziomej asymptoty .. y=−1 ? nalezy jeszcze określić dziedzinę oraz zbiór wartości funkcji i i podać y>0 dla x y<0 dla x