Podaj liczbę rozwiązań w zależności od parametru m. pytacz: Podaj liczbę rozwiązań w zależności od parametru m. |x−2|=2m+1 Czy mógłby mnie ktoś chociaż naprowadzić? Z góry dziękuje.

Eta: 0 rozwiązań dla 2m+1 <0 ⇒ m<......... 1 rozwiązanie dla 2m+1=0 ⇒m=..... 2 rozwiązania dla 2m+1 >0 ⇒ m>.........

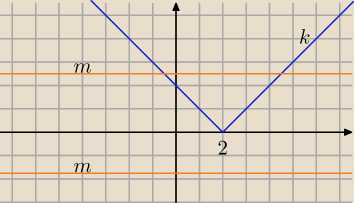
Bogdan: Wykres k: y = |x − 2| Wykres m: y = 2m + 1, to jest wykres funkcji stałej, Wykresy k i m mogą się nie przecinać (gdzie?), mogą się przecinać w jednym punkcie (gdzie?) oraz mogą sie przecinać w dwóch punktach (gdzie?).

pytacz: No tak, nie pomyślałem, że więcej rozwiązań nie osiągnie. Późno już. ^^

pytacz: y=2m+1 to wykres funkcji stałej?

asdf: ta

pytacz: A skąd to wiemy?

5-latek: Przeciez m jest tez liczba −−−−parametr jest liczba jesli do y=2m+1 wstawimy za m=2 to otrzymamy y=2*2+1 to y=5 Teraz popatrz na wykres Bogdana i zobacz ze dla m=2 to rownanie ma 2 rozwiazania bo wykres funkcji y=5 przecina w dwoch miejscach wykres funkcji y=|x−2| A np dla m=−10 ile bedzie rozwiazan?