geometria analityczna ppp: punkt A=(−4,1),B=(−1,−2) sa kolejnymi wierzcholkami rombu ABCD. punkt C lezy na prostej x + y − 3 = 0. Znajdz rownanie prostej CB ja porownalem odcinek AB i odleglosc punkt B od prostej y = −x +3 , wychodzi tyle samo ,wiec prosta to y = x + b , gdzie b bez problemu wylicze z punku B(−1,−2) Ale gdyby proste nie byly prostopadle, to nie wiem jak to zrobic, moze wy mi pomozecie ?

Beti: wg mnie, aby wyznaczyć wsp. pktu C należy zauważyć, że: 1) pkt C leży na danej prostej, więc: C = (x, 3−x) 2) romb ma wszystkie boki tej samej długości, więc: AB = BC , czyli: √(−1+4)²+(−2−1)² = √(x+1)²+(3−x+2)² teraz wystarczy rozwiązać równanie i obliczyć wsp. punktu C Prostą BC łatwo już będzie wtedy wyznaczyć

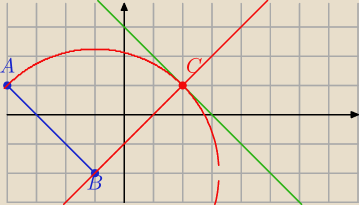
Mila: Punkt C leży na prostej x + y − 3 = 0. Znajdź równanie prostej CB. m: y=−x+3 A=(−4,1),B=(−1,−2) C=(x,−x+3) |AB|=√3²+3²=3√2 "Kreślimy" okrąg o środku B=(−1,−2) i promieniu R=3√2 (x+1)²+(y+2)²=18 Jest jeden punkt przecięcia z prostą y=−x+3 rozwiązujemy układ: (x+1)²+(y+2)²=18 i y=−x+3 x²+2x+1+(−x+3+2)²=18 x²+2x+1+x²−10x+25−18=0 2x²−8x+8=0 x²−4x+4=0 (x−2)²=0 x=2 y=−2+3=1 C=(2,1) Prosta BC: y=ax+b 1=2a+b −2=−1a+b odejmuję stronami: 3=3a a=1, b=−1 BC: y=x−1

Bogdan: prosta k₁: x + y − 3 = 0 ⇒ y = −x + 3, a₁ = −1

	−1
prosta k2: y = a2x + b2, B(−1, −2)∊k2, k2⊥k1 ⇒ a2 =		= 1
	a1

k₂: y = 1(x + 1) − 2 ⇒ y = x − 1

Eta:

ppp: dzieki

Mila: Oczywiście, lepiej byłoby, gdybym to pokazała, gdy punkt C leży na prostej np. y=−x+2. Spróbuj sam rozwiązać.W razie kłopotów, jutro sprostujemy.