Równanie okręgu Monika: Wyznacz równanie okręgu o NAJMNIEJSZYM możliwym promieniu stycznego do okręgu x² + y² = 5 i prostej y=2x−10.

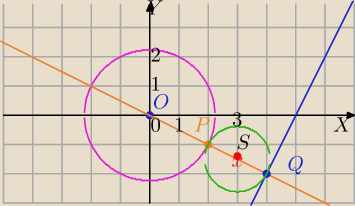
Mila: x² + y² = 5 , R=√5 k: y=2x−10 Obliczamy odległość punktu O od prostej k 2x−y−10=0

	10
d=U{|2*0−0−10|}{√22+12=		=2√5
	√5

Odległość prostej od okręgu=2√5−R=√5

	1
r=		√5 promień okręgu stycznego do prostej k i okręgu.
	2

środek leży na prostopadłej do k i przechodzącej przez punkt (0,0)

	−1
m: y=ax i a=
	2

	−1
y=		x
	2

Szukamy puntu przecięcia prostej m z okręgiem i prostą k.

	−1
x2+(		x)2=5
	2

5
	x2=5
4

x²=4 i x>0 x=2 lub x=−2 nie odpowiada założeniom

	−1
y=		*2=−1
	2

P=(2,−1)

−1
	x=2x−10
2

x=4 , y=−2 Q=(4,−2)

	2+4		−1−2		−3
S=(		,		)=(3,		)
	2		2		2

	3		5
(x−3)2+(y+		)2)=
	2		4