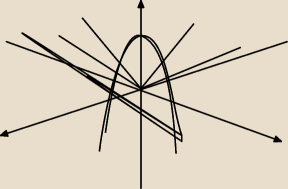
Całki podwójne Zgrabny: Witam, mam do policzenia objętość bryły ograniczonej powierzchniami z=6−x²−y², z=√x²+y². (nie patrzcie na to coś co mi z boku się narysowało, nie wiem co to ) moje pytanie takie.. Jaki jest rzut na plaszczyzne xy? bo to bedzie kolo, ale nie znam jego rownania.. mam przyrownac te dwa rownania? ale wtedy nie wiem jak to rozwiazac. Prosze o pomoc

Zgrabny: Bo bryła bedzie wygladac tak, prawda? to jak teraz obszar znalezc.

Zgrabny: Ktoś ma pomysł?

Zgrabny: HMM

Krzysiek: przejdź na współrzędne biegunowe i wylicz promień: z=5−r² z=r r=5−r² i wtedy będziesz wiedział jaki to będzie rzut na płaszczyznę xy.

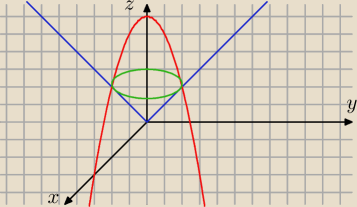
Trivial: Prosty sposób jak tę bryłę narysować: 1. Przejdź na współrzędne biegunowe: z = 6 − r², z = r. 2. Przyjmij x = 0, wtedy r = √x² + y² = |y| = y (dla y ≥ 0). 3. Narysuj te wykresy i obróć wokół osi z.