Dla jakich wartości parametru m dana prosta jest styczna do okręgu? Monika: Dla jakich wartości parametru m prosta 3x+4y=0 jest styczna do okręgu x² + y² + 6x −2my = 16 − m² . Zrobiłam układ równań z tych prostych. Ale chyba źle wyszło: ²⁵₉ y² + y(8−2m) + m² − 16=0 I dalej chyba trzeba deltę obliczyć, a potem do zera przyrównać, ale nie wychodzi mi dobry wynik. Mógłby ktoś z obliczeniami napisac? Gubię się w tych obliczeniach chyba

asdf: x² + y² + 6x −2my = 16 − m² // + 9 x² + 6x + 9 + y² −2my= 25 − m² // + m² (x+3)² + y² − 2my + m² = 25 (x+3)² + (y−m)² = 25 S(−3,m), r = 5 teraz musisz znaleźć taki środek, gdzie odległość środka będzie = 5 od prostej 3x + 4y = 0

Patryk: albo wylicz y z 3x+4y=0 wstaw tego y do równania okręgu i plicz Δ temu równaniu a następnie przyrównaj do zera i wylicz m

Monika: ale jak podstawić to do równania okręgu? Za x coś podstawić? Nie rozumiem...

Monika: asdf: czemu tam dodałaś/łeś 9?

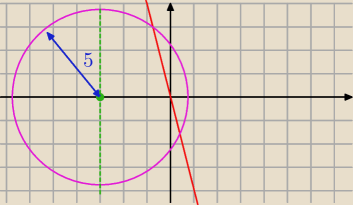
asdf: x już masz, teraz musisz znaleźć taki punkt m, który będzie oddalony od prostej: 3x + 4y = 0 o 5 jednostek. Tak lopatologicznie to te "kólko" na pewno sie porusza po zielonej prostej "x=3", teraz trzeba "dopasowac" tak, by sie stykał z czerwoną prostą.

asdf: bo zauwazylem wzor skroconego mnozenia

Monika: Dziękuję. Już rozumiem.. Mam nadzieję, że wynik mi dobrze wyszedł.

asdf: mozesz zrobic tak jak napisal Patryk, albo po prostu obrać punkt (juz sie powtarzam) (−3,m). gdzie m to wspolrzedna y, skorzystac ze wzoru na odleglosc punktu od prostej i przyrownac do 5: Odległość punktu od prostej: http://www.youtube.com/watch?v=6TGEqnv-hgM

asdf: jak nie jestes pewna to podaj wynik, szybko sprawdze

Monika: m= 8 ¹₂ ∨ m= −4

asdf:

Monika: Wielkie dzięki

asdf: proszę