okrąg i prosta piotrek221: Prosta y=−x−6 przecina okrąg x²+y²=20 w punktach A i B. Oblicz długość cięciwy AB.

bibi: Musisz równanie prostej i okręgu wziąć w układ równań − będą 2 pary rozwiązań (x,y), które wskazują punkty wspólne prostej i okręgu, a zarazem są końcami cięciwy. No i na koniec współrzędne tych punktów należy wstawić do wzoru na długość odcinka o znanych współrzędnych końców.

dero2005:

⎧	x2+y2=20
⎩	y=−x−6

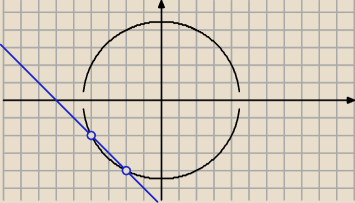
Δ = 16 x₁ = −4 x₂ = −2 y₁ = −2 y₂ = −4

dero2005: d = √(x₂−x₁)²+(y₂−y₁)² → odległość między punktami