Układy nierówności Minis: Witam pytanie odnośnie zadnia Na matmie przerabiamy teraz nierówność pierwszego stopnia z dwiema niewiadomymi i jej interpretacją geometryczną. Zaznacz w układzie współrzędnych zbiór punktów, których współrzędne spełniają dany układ nierówności: x−y ≤ 1 1/2x+2y ≥ −1 y−1/2x−1≤0 (to jest w jednym układzie, ale nie umiem zrobić klamry ) I aby zrobić to zadanie muszę przekształcić te nierówności w: y ≥ x−1 y ≥ −1/4x−1/2 y ≤ 1/2x+1 (to także w klamrze) I potem powinienem podstawić losowe pkt, np (0,1) i narysować w układzie ? Jak to powinno teraz wyglądać ?

Tadeusz: ... po co Ci ten punkt ? Rysuj proste i zaznaczaj obszary −

Minis: Ale jak narysuje prostą mając sam wzór ?

Tadeusz: ... a co Ci więcej potrzeba?

Minis: To jak ma wyglądać prosta y≥x−1 w układzie współrzędnych ? Możesz wytłumaczyć jak dla ułomnego, bo już trochę czasu robię zadania i mój mózg nie działa jak trzeba

dero2005:

Minis: Dzięki, ale jak to narysowałeś ?

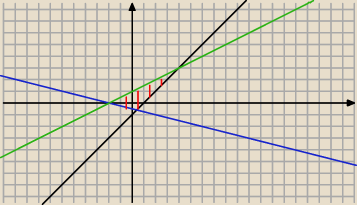
dero2005: y = x−1 półpłaszczyzna w "górę" łącznie z prostą (≥) y = −¹₄x−¹₂ półpłaszczyzna w "górę" łącznie z prostą (≥) y = ¹₂x+1 półpłaszcyzna w "dół" łącznie z prostą (≤) obszar wspólny trzech półpłaszczyzn daje nam pole zakreskowane czerwone

Minis: No tak ,jak najbardziej racja, ale jak je tam umiejscowiłeś, wybrałeś losowe pkt, podstawiłeś do równania i wybrałeś ?

dero2005: wyznaczasz co najmniej dwa punkty i kreślisz przez nie linię prostą i tak robisz z każdą funkcją liniową

Minis: Dzięki, o to mi chodziło i właśnie zrobiłem jeden z trudniejszych podpunktów w zadaniu. Dzięki za pomoc