funkcja kwadratowa fan 2: Wyznacz postac ogólną i iloczynową funkcji kwadratowej, o której wiadomo, że dla argumentu 3 osiąga najmniejszą wartośc równą −8, a jednym z miejsc zerowych jest liczba 5. Pomocy, sprawdzianik niedługo a ja chory w domu. doszedłem do tego, że Wierzchołek(3,−8) i dalej nie wiem na ugryzc te zadanko. Proszę o pomoc.

tim: Masz wierzchołek (3, −8) i jeden punkt A (5, 0). Zatem postać kanoniczna będzie wyglądała tak: y = a(x − 3)² − 8 Podstawiając punkt A do wzoru wyliczamy a. 0 = a(5 − 3)² − 8 0 = 4a − 8 4a = 8 a = 2 y = 2(x − 3)² − 8 Wystarczy przekształcić wzór: y = 2(x² − 6x + 9) − 8 y = 2x² − 12x + 18 − 8 y = 2x² − 12x + 10

fan 2: Dzieki wielkie za wytłumaczenie

tim: Nie ma problemu Ważne, żebyś zrozumiał.

fan 2: No, trzeba wpaśc na pomysł i reszta leci z górki ^^

fan 2: Tylko jeszcze ejdno pytanko: O tutaj−−>Podstawiając punkt A do wzoru wyliczamy a. 0 = a(5 − 3)2 − 8 Gdy podstawiamy jeden np. x z jednej danej, a y z innego pkt. np. −8 czy było by to właściwe? czy trzeba uważac z tym dopasowywaniem liczb ?

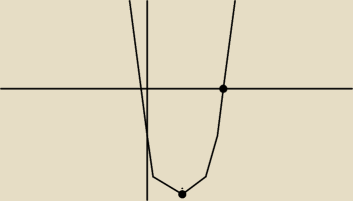
tim: Masz dwa punkty: W wierzchołek, który możemy wyczytać z postaci kanonicznej, jak również utworzyć wzór na podstawie wierzchołka. A − punkt dowolny, który podstawiamy (x oraz y punktu A) do wzoru wyżej i obliczamy współczynnik.