ciągłość MOnika:

	1
Czy funkcja wymierna		dla n∊N jest funkcją ciągłą? gdzie x∊[0,+∞)
	1+nx

.ee: Rozwiaz rownanie mianownik = zero. Co spostrzegasz?

MOnika: nie jest wymierna w punkcie 0 tak? 1+nx=0 x=−1/n

asdf: jest ciagla

MOnika: ale jak?

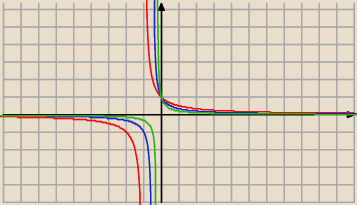
asdf: n jest dodatnie, x jest także dodatnie, czyli: n * x > 0, zapiszę to jako x⁺ 1 + x⁺ = 0 zeruje się to w miejscu x⁺= −1, ale x⁺ jest dodatnie, czyli sprzeczność. Wniosek: zawsze jest ciągła. dowód graficzny:

	1
y =
	1+x

	1
y =
	1+2x

	1
y =
	1+4x

(...) dla x ≥ 0 zawsze jest ciągła P.S Ciągłość funkcji jako tako jest niemozliwe do wykazania, tak jak liczenie calki z definicji, ale "na zdrowy rozsadek" to wszystko się zgadza.

MOnika: Mam takie zadanie. Zbadać zbieżność ciągu funkcyjnego:

	1
fn(x)=		x∊[0,∞)
	1+nx

	1
fn(0)=1 a limn→∞		=0 ⇒ fn→f.
	1+nx

To f jest funkcją nie ciągłą?

MOnika:

asdf: ...takie podejście..przepisujesz polowe, ja sie glowie nad tym o co Ci chodzi, dopiero pozniej przepisujesz reszte − sama sobie licz teraz.

MOnika: no właśnie nie rozumiem dlaczego jest napisane że nie jest ciągła?