log_x^2-1 ss: log_x²₋₁(x²−2x−3) (x−1)(x+1)>0 x=1 x=−1 x²≠2 √2 i −√2 x₁=3 x₂=−1 mógłby ktoś narysować to na osi ?

wredulus_pospolitus: 1) gdzie jest podana dziedzina ciebie chyba pokiełbasiło, że ktoś narysuje to 'monstrum' bez zrobienia badania przebiegu zmienności funkcji

ICSP: wredulus on ma określić dziedzinę oraz chce aby narysować mu na osi założenia do dziedziny 1^o x ∊ (− ∞ ; −1) ∪ (1 ; + ∞) 2^o x ≠ ± √2 3^o x ∊ (−∞ ; −1] ∪ [3 ; + ∞)

wredulus_pospolitus: ehhh ... ja chyba coraz starszy jestem ... coraz mniej i mniej rozumiem 'młodziaków'

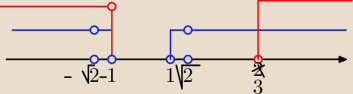
Basia: 1. ma być (x−1)(x+1)>0 czyli x∊(−∞;−1)∪(1;+∞) ale to za mało jeszcze musi być 2. x²−1 ≠ 1 ⇔ x²≠2 ⇔ x≠ −√2 i x≠√2 czyli teraz mamy x∊(−∞;−√2)∪(−√2;−1)∪(1;√2)∪(√2;+∞) i musi być 3. x²−2x−3>0 ⇔ (x+1)(x−3)>0 ⇔ x∊(−∞;−1)∪(3;+∞) część wspólna: (−∞;−√2)∪(−√2;−1)∪(3;+∞)

Basia: ICSP skąd domknięcie przy 3 ?

ICSP: Nie wiem skąd Oczywiście powinny być otwarte : 3^o x ∊ (−∞ ; −1) ∪ (3 ; + ∞) Dziękuję Basiu za zwrócenie uwagi

Basia: wiesz, mnie się ostatnio taki idiotyzm udało napisać, że zwątpiłam i tym razem w siebie miewamy takie dni