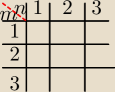
Relacje Majk: Zdefiniowana jest relacja m ρ n ⇔ m ≡ n ( mod 2) I należy uzupełnić tabelkę opisująca daną relacje.

wredulus_pospolitus: 1 ≡ 1 (mod 2) 1 ≡ 3 (mod 2) 2 ≡ 2 (mod 2) a zapis: 3 ≡ 1 (mod 2) jest nieprawidłowy −−− to tak aby nie było wątpliwości

wredulus_pospolitus: tak samo jak: 3 ≡ 3 (mod 2)

Majk: tylko co będzie w tabelce ? 1 ≡ 1 (mod 2) −> w tabelce 1 ? 1 ≡ 3 (mod 2) −> w tabelce 1 ? 2 ≡ 2 (mod 2) −> w tabelce 1 ? Skad mam wiedzieć czy w tabelce wpisać 0 czy 1 ?

wredulus_pospolitus: 0 −−− fałsz 1 −−− prawda

Majk: Tak to wiem, tylko nie wiem jak to się sprawdza w tym działaniu. Jak to się liczy? Np. 3 ≡ 1 (mod 2) i co mi mówi ten zapis? jak sprawdzić kiedy jest fałsz a kiedy prawda?

ICSP: Wiesz co oznacza zapis mod 2 ?

Basia: jaka jest reszta z dzielenia 3 przez 2 ? 1 jaka jest reszta z dzielenie 1 przez 2 ? też 1 zatem 3≡1 (mod2) liczby przystają do siebie mod(n) jeżeli reszty z ich dzielenia przez n są takie same

Majk: wiem co znaczy samo mod 2 tylko nie wiem jak mam rozumieć ten zapis ( np.3 ≡ 1 (mod 2) ) i jak go ewentualnie rozwiązać żeby sprawdzić czy jest prawda czy fałsz.

Basia: toż Ci napisałam

Majk: Ale jakimś skomplikowanym językiem Ok, ale chyba zrozumiałem Zaraz napisze i mi dajcie znać czy dobrze rozumiem

Basia: @wredulus wg mnie relacja przystawania modulo jest relacją równoważności więc jest symetryczna

Majk: 1 ≡ 1 (mod 2) −> w tabelce 1 ? 1 ≡ 2 (mod 2) −> w tabelce 0 ? 1 ≡ 3 (mod 2) −> w tabelce 1 ? 2 ≡ 1 (mod 2) −> w tabelce 0 ? 2 ≡ 2 (mod 2) −> w tabelce 1 ? 2 ≡ 3 (mod 2) −> w tabelce 0 ? 3 ≡ 1 (mod 2) −> w tabelce 1 ? 3 ≡ 2 (mod 2) −> w tabelce 0 ? 3 ≡ 3 (mod 2) −> w tabelce 1 ?

Basia: wg mnie tak ale niech się jeszcze wredulus wypowie

wredulus_pospolitus: Basiu oczywiście masz rację ... przystawanie pomyliłem ze zwykłym równa się ... gdzie oczywiście symetrii brak