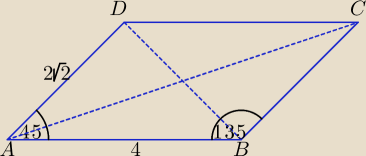
Twierdzenie cosinusów kasia: Dane są długości a, b dwóch sąsiednich boków równoległoboku oraz kąt gamma zawarty między tymi bokami. Oblicz długość przekątnych tego równoległoboku. a=4, b=2√2 γ=45^o Jedna przekątna wyszła mi 2√2, ale jak mam się za drugą zabrać? Powinna wyjść taka sama, bo 180−45=135 To cos 135^o = 90+45 czyli −sin45^o. Może ktoś pomóc rozwiązać mi to zadanie?

Eta: e²+f²=2a²+2b² ⇒ f²= 2a²+2b²−e² e²= 8 f=..........

Eta:

	√2
lub cos135o = cos(180o−45o) = −cos45o= −
	2

	√2
f2= 42+(2√2)2+2*4*2√2*
	2

f=.........

kasia: Co to za wzory?

Ajtek: Redukcyjne.... Dobry wieczór "miś"

bezendu: miś

kasia: e2+f2=2a2+2b2 mówie o tych, redukcyjne znam i używam, ale mimo wszystko nie wychodzi taki wynik jaki jest podany w książce czyli 2√10

Bogdan:

	1		1
cos45o =		, cos135o = −
	√2		√2

Z twierdzenia cosinusów:

	1
|BD|2 = 16 + 8 − 2*4*2√2*		= 8 ⇒ |BD| = 2√2
	√2

	1
|AC|2 = 16 + 8 + 2*4*2√2*		= 40 ⇒ |AC| = 2√10
	√2

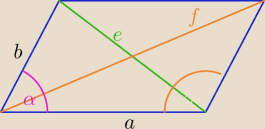
Eta: cosβ= cos(180^o−α)= −cosα z tw. cosinusów e²=a²+b²−2ab*cosα f²= a²+b²+2ab*cosα +−−−−−−−−−−−−−−−−−−−−−− e²+f²= 2a²+2b² ( dla każdego równoległoboku zachodzi taki wzór!

kasia: Wcześniej się z nim nie spotkałam, wybaczcie. Poradziłam już sobie, dzięki wielkie

Eta:

Ajtek: I Dwoje Mistrzów dało popis wiedzy . Dobry wieczór Bogdan .

Eta:

Ajtek: "miś nie mrugaj tak na mnie okiem .

Bogdan: Dobry wieczór