Tw. sinusów Alk: Jak udowodnić twierdzenie sinusów w przypadku gdy rozpatrywanym trójkątem jest trójkąt rozwartokątny?

PW: Rozumiem, że na lekcji było dla prostokątnego i ostrokątnego, a to jest praca domowa?

AS:

	1
Wykorzystuję wzór na pole trójkąta P =		a*b*sin(γ)
	2

1		1
	a*c*sin(β) =		b*c*sin(α)
2		2

a*sin(β) = b*sin(α)

a		sin(α)
	=
b		sin(β)

Podobnie powtórzyć dla pary boków b i c

Alk: a mógłbyś mi to też napisać? byłbym wdzięczny

PW: Narysuj trójkąt rozwartokątny wpisany w okrąg. Narysuj inny trójkąt, który nie jest rozwartokątny, ale ma bok a taki sam jak ten pierwszy trójkąt. Żeby uniknąć dyskusji najlepiej wziąć taki, którego jednym z boków jest średnica okręgu, wtedy na pewno wiemy, że jest prostokątny. A dla prostokątnego już wiemy: U{a}{sinα)=2R Jest to typowe postępowanie w dowodzeniu: żeby udowodnić trudniejszy − nieznany przypadek sprowadzamy go do już znanego. Dlatego pytałem, czy na lekcji były te łatwiejsze przypadki. Nie mówię, że rozumowanie AS jest złe, ale tu na pewno szło o dokończenie dowodu twierdzenia sinusów jednolitą metodą, opartą na spostrzeżeniu, że kąty wpisane oparte na tym samym łuku są równe.

Alk: Cholera, mało to rozumiem, nighdy nie byłem dobry z geometrii . Mógłby mi to ktoś narysować i pokazać?

PW: Nie umiem tutaj rysować, dostałbym furii. Co narysuję jakimś cudem okrąg i chcę dorysować trójkąt, to okrąg ginie. Chyba jestem mało inteligentny. W wielu programach graficznych sobie radzę od 20 lat, a tu nie potrafię.

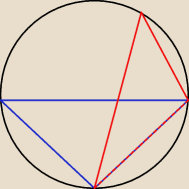
Nienor: Oto chodzi PW Koło znika bo próbujesz rysować za duże, takie, żeby dotawało do brzegów, a tak nie wolno.

PW: Dzięki, tak właśnie było, bo źle widzę i mam tendencje do rysowania duuużych ilustracji. Stanowczo jednak wolałbym zrobić rysunek gdzie indziej i tu wstawić *.png czy *.eps.