Przekroje ostrosłupów
Arek: Ostrosłup prawidłowy czworokątny, którego wszystkie krawędzie mają długość a, przecięto
płaszczyzną zawierającą dwie wysokości ścian bocznych poprowadzone z wierzchołka ostrosłupa.
Oblicz pole otrzymanego przekroju
19 wrz 18:57
Arek: Jakby ktoś mógł pomóc

19 wrz 19:34
Bogdan:
Najpierw Twój rysunek i Twoja propozycja rozwiązania
19 wrz 19:36
dero2005:
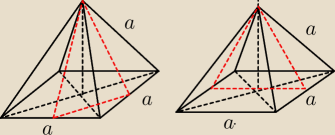
19 wrz 19:49
Arek:
19 wrz 19:50
Arek: Jakaś dokładniejsza pomoc?

19 wrz 20:40
dero2005:
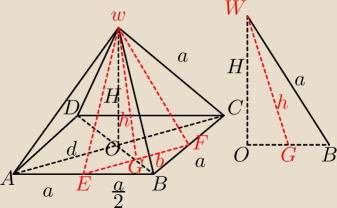
| | a√2 | |
|EF| = b = √(a2)2 + (a2)2 = |
| |
| | 2 | |
|AC| = d = a
√2
| | a√2 | |
H = √a2 − (a√22)2 = |
| |
| | 2 | |
| | a√6 | |
|GW| = h = √|OG|2 + H2 = |
| |
| | 4 | |
19 wrz 21:28
dero2005:
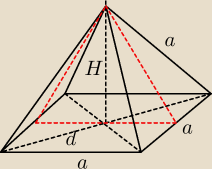
d = a
√2
| | a√2 | |
H = √a2 − (a√22)2 = |
| |
| | 2 | |
który przypadek Cię interesuje?
19 wrz 21:33


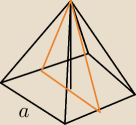


 d = a√2
d = a√2