Ostrosłup prawidłowy/przekroje Arek: Przez krawędź podstawy ostrosłupa prawidłowego czworokątnego poprowadzono płaszczyznę prostopadłą do przeciwległej ściany bocznej. Oblicz pole otrzymanego przekroju, jeśli długość krawędzi podstawy i krawędzi bocznej tego ostrosłupa wynoszą odpowiednio 10 i 13

Arek: Wiem, że zadanie trudne, no ale...

Arek: pomoże ktoś?

Arek: trudne?

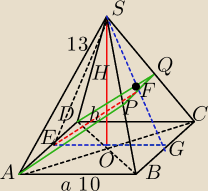
Mila: EF jest wysokością w ΔEGS.

	1
|OB|=		a√2=5√2
	2

H²+|OB|²=|SB|² H²=13²−(5√2)² H²=169−50 H²=119 H=√119 W ΔSOG: |SG|²=H²+|OG|² |SG|²=√119²+5² SG=12

	EF		H		h
ΔEFG∼SOG⇔		=		⇔		=√119{12}
	EG		SG		10

h=... Oblicz FG, potem SF i z podobieństwa ΔSPQ i ΔSBC oblicz PQ Dokończ