Ostrosłup Arek: Ostrosłup prawidłowy trójkątny ABCS, gdzie S jest wierzchołkiem ostrosłupa o krawędzi podstawy a i kącie między krawędzią boczną i krawędzią podstawy α przecięto płaszczyzną przechodzącą przez środki krawędzi bocznych BS i CS oraz wierzchołek A. Oblicz pole otrzymanego przekroju.

Arek: Potrafi ktoś to rozwalić?

Arek: Ktokolwiek?

Arek: Pomoże ktoś?

Nienor: To jest nie tyle trudne, co strasznie żmudne, do tego wychodzą zwykle długie i poplątane wyniki, w któych, zwłaszcza pisząc na komputerze można się pogubić.

Arek: To może rozwiązanie z kartki na maila venom11@o2.pl? może być nawet takie podstawowe które potem bym sobie do końca policzył

Mila:

	1
DE=		a
	2

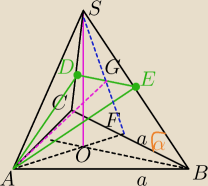
(odcinek łączący środki dwóch boków trójkąta jest równoległy do boku trzeciego i równy połowie tego boku) GA=h − wysokość ΔDEA

	1
|GF|=		|SF|
	2

W ΔSFB:

	|SF|
tgα=
	0,5a

	1
|SF|=		a*tgα
	2

	1
|GF|=		a*tgα
	4

	OF		1   a√3 6		√3ctgα
cos∡OFS=		=		=
	SF		1   a*tgα 2		3

	√3ctgα
AG2=AF2+GF2−2*AF*GF*
	3

Spróbuj dalej sam, jeśli masz odpowiedź to podaj, pisz w razie trudności.

Arek: Dzięki, rozwiązałem do końca i wyszło jak w odpowiedzi

Mila: