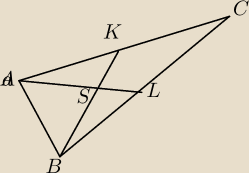
 Podstawą trójkąta równoramiennego ABC jest bok AB. Środkowe AL i BK przecinają się w punkcie S
pod kątem 60 stopni( kąt ASB). Wiadomo, że pole trójkąta ABS jest równe √3.
a) oblicz długość boków trójkąta ABC,
b) Czy kąt ACB jest róny 30 stopni? odp uzasadnij.
w odp. jest tak: a) AB=2, AC=BC=2√7; b) sin kątaACB= 3√3/14, wiec acb<30 stopni
Podstawą trójkąta równoramiennego ABC jest bok AB. Środkowe AL i BK przecinają się w punkcie S
pod kątem 60 stopni( kąt ASB). Wiadomo, że pole trójkąta ABS jest równe √3.
a) oblicz długość boków trójkąta ABC,
b) Czy kąt ACB jest róny 30 stopni? odp uzasadnij.
w odp. jest tak: a) AB=2, AC=BC=2√7; b) sin kątaACB= 3√3/14, wiec acb<30 stopni
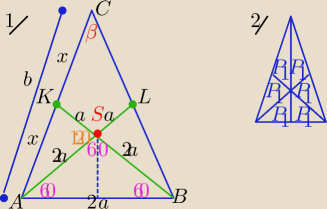 Trzy środkowe dzielą trójkąt na sześć trójkątów o równych polach (rys, 2)
Trzy środkowe dzielą trójkąt na sześć trójkątów o równych polach (rys, 2)
| √3 | ||
P(ΔABS)= √3 to P(ΔABC)= 6* | = 3√3 | |
| 2 |
| 2a)2√3 | ||
trójkąt ABS jest równoboczny ⇒ P= | = √3 ⇒ 2a=|AB|=2 | |
| 4 |
| 1 | ||
cos120o= −cos60o= − | ||
| 2 |
| 1 | 3√3 | |||
P(ΔABC)= | *b*b*sinβ ⇒ 3√3= 2*7*sinβ ⇒ sinβ= | ≈ 0,37 | ||
| 2 | 14 |
 Dobranoc Wszystkim "nocnym Markom"
Dobranoc Wszystkim "nocnym Markom" 


