matma Asiq: Oblicz współrzędne punktu przecięcia się symetralnych odcinków AB i CD, gdy A=(−2,−1) , B= (4,2), C =(1,1) i D = ( 3, −3)

PW: Symetralna jest prostopadła do odcinka i przechodzi przez jego środek. Umiesz wyliczyć środki? A napisać równanie prostej prostopadłej do wektora? To jesteś na dobrej drodze.

Asiq: środki z AB i CD umiem, ale to drugie nie za bardzo prosze mi przybliżyć ...

PW: Prosta prostopadła do wektora [K,L] ma równanie Kx+Ly+C=0. Było? Bo jeśli nie, to trzeba inaczej (będzie więcej rachunków).

Asiq: Było i co dalej?

Asiq: to czasami nie było Ax + By+C=0 równanie ogólnej prostej o to chodzi?

Asiq: mam obie te współrzędne podstawić?

debhil3: ΔβπΩ∑←

Asiq:

PW: Wyliczyć współrzędne wektora AB^→=[K,L] (teraz widzisz dlaczego napisałem równanie ogólne prostej używając innych literek) − to będą owe "współrzędne wektora prostopadłego do szukanej symetralnej". Zostanie niewiadoma C (też należałoby użyć innej literki, np. M), a ją obliczymy podstawiając do równania Kx+Ly+M=0 współrzędne środka odcinka (bo środek należy do symetralnej).

Asiq: jak na przykład wyszły mi współrzędne odcinka AB S= ( 1 , 0,5) to będzie : 1 + 0,5 + M = 0 to M = −1,5 tak samo w drugim CD : S = (2, −1) 2 − 1 + M = 0 M =−1 A potem Wogule dobrze?

PW: [K,L]=[AB^→]=[4−(−2),2−(−1)]=[6,3], czyli K=6, L=3. Szukamy M: w równaniu 6x+3y+M=0

	1
podstawiamy współrzędne środka S: x = 1 i y=
	2

	1
6•1+3•		+M = 0
	2

	15
M = −
	2

Równanie symetralnej odcinka AB ma postać:

	15
6x+3y−		=0
	2

(można wymnożyć przez 2, ale obowiązku nie ma). Ta sama czynność dla wektora [CD^→]=[3−1,−3−1] i środka S'=(2,−1) odcinka CD. Po wyznaczeniu równania tej drugiej symetralnej liczymy współrzędne punktu, w którym symetralne przecinają się.

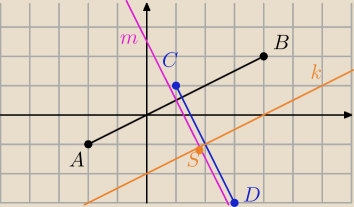
Mila: A=(−2,−1) , B= (4,2), C =(1,1) i D = ( 3, −3) 1) symetralna AB − zbiór punktów P(x,y) jednakowo odległych od końców odcinka AB √(x+2)²+(y+1)²=√(x−4)²+(y−2)² /² (x+2)²+(y+1)²=(x−4)²+(y−2)² x²+4x+4+y²+2y+1=x²−8x+16+y²−4y+4 ⇔m: y=−2x+2,5 2) symetralna CD− zbiór punktów P(x,y) jednakowo odległych od końców odcinka CD⇔ √(x−1)²+(y−1)²=√(x−3)²+(y+3)² /²⇔ x²−2x+1+y²−2y+1=x²−6x+9+y²+6y+9

	1
⇔k: y=		x−2
	2

Punkt przecięcia

	1
		x−2=−2x+2,5
	2

	9
x=
	5

y=−1,1

	9
S=(		;1,1)
	5

Sprawdź rachunki.

PW: Równanie y=−2x+2,5 pierwszym sposobem otrzymaliśmy − zapisane w postaci ogólnej. Drugie równanie prostej też (po wykonaniu rachunków) takie jak trza. Mamy czyste sumienie − oba sposoby dają to samo.

Marty: Jesteś fajna dzięki