Monotoniczność i ekstermum funkcji pyśka: Mam funkcję: f(x)= x/ x² +1 policzyłam z tego pierwszą pochodną gdzie mi wyszło: f'(x)= −x² +1/ (x² +1)² Przyrównałam licznik do zera: czyli, −x²+1=0 x=1 i na rysunku ma być parabola o gałęziach skierowanych w dół ale jak mam policzyć monotoniczność i ekstrema?

Tad: ... idziesz po ścieżce ... to dobrze jeszcze wiedzieć gdzie w danej chwili jesteś − Liczysz pochodną i przyrównując do 0 sprawdzasz jeden z warunków ... a drugi warunek ? −

pyśka: jaki drugi warunek?

Janek191: − x² + 1 = 0 ⇔ x = − 1 ∨ x = 1

pyśka: aha czyli monotoniczność bedzie jaka?

Tad: ... poczytaj o warunkach istnienia ekstremum ... −

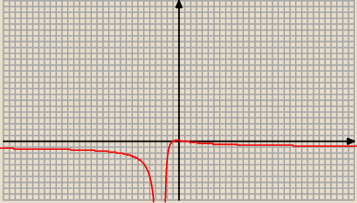Janek191: Z wykresu odczytujemy znak pochodnej w otoczeniu x = − 1 , a następnie x = 1 : x < − 1 ⇒ y ' <0 x = − 1 ⇒ y' = 0 x > − 1 ⇒ y' > 0

	x
Funkcja f(x) =		ma w x = −1 minimum lokalne
	x2 + 1

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− x < 1 ⇒ y' > 0 x = 1 ⇒ y' = 0 x > 1 ⇒ y' < 0 Funkcja f ma w x = 1 maksimum lokalne −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−