badanie funkcji.. za 2 dni poprawka.. pomocy! soni87: f(x)=x/(x−2) DfxeR\{2} pochodna to f'(x)=[x'(x−2)−(x)(x−2)'] / (x−2)²= −2/(x−2)² co dalej mam zbadac monotonicznosc funkcji i ekstremum lokalne

Nienor: Pytasz o algorytm, czy jak dalej w tym przykładzie Badanie monotoniczności: Jeżeli f'(x)<0 funkcja f(x) maleje, kiedy f'(x)>0 funkcja rośnie. Wystarczy zbadać znak pochodnej:

−2
	>0
(x−2)2

−2(x−2)²>0 → (funkcja kwadratowa ramiona w dół, 1 pierwiastek, czyli nie ma wartości dodatnich) f'(x)<0 dla x∊(−∞,2)∪(2,+∞) ⇒ f↘ dla x∊(−∞,2)∪(2,+∞) f(x) może (ale nie musi) mieć ekstrema tylko, gdy f'(x)=0. Jeżeli funkcja w miejscu zerowania się pochodnej zmienia swoją monotoniczność (czyli najpierw rośnie, później maleje lub na odwrót) to możesz odrazu pisać, że jest to miejsce zerowe. W innym wypadku musisz policzyć drugą pochodną. Jeżeli ona się zeruje w tym samym x, to jest ten x miejscem przegięcia funkcji, a nie ekstremum (jak x=0, przy funkcji f(x)=x³). W tym wypadku f'(x)=0 nie ma rozwiązania (x=2 wypada z dziedziny zarówno pochodnej, jak i funkcji). Gdy zdarzy się sytuacja, że ten x wypada tylko z dziedziny pochodnej, to możesz napisać, że jest tam ostrze (Szpic jak przy funkcji f(x)=|x|).

soni87: aha.. pytam o to jak sie rozwiazuje te zadania ... mase czasu spedzilem na korepetycjach ale jak siadam do zadan z ksiazki i wychodzi mi cos innego niz w odpowiedziach.... a co z tym f(x)=x³ *e^x Df=xnR pochodna wyliczylem.. f'(x)=e^x(3x²+X³) wiedzac ze funkcja e^x stale rośnie to nie ma minimum lokalnego?

Nienor: Nie, e^x nie ma wpływu na znak, bo zawsze jest dodatnie, więc możesz je zaniedbać. 3x²+x³>0 x²(x+3)>0 f(x)↗ dla x∊(−3,+∞) f(x)↘ dla x∊(−∞,−3) czyli x=−3 jest ekstremum, co do x=0 nie jesteśmy pewni. Badamy więc dalej: f''(x)=6xe²+3x²e^x+3x²e^x+x³e^x=e^x(x³+6x²+6x) Znów zaniedbujemy e^x: x(x²+6x+6)=0 ⇔ x=0 ∨ x²+6x+6=0 Jak widać dla x=0 zeruje się druga pochodna, jest to więc punkt przegięcia funkcji, nie ekstremum.

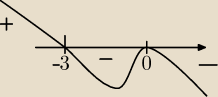
soni87: tak powinien wygladac wykres? jak mamy x² przed nawiasem to traktujemy jak zero?