Oblicz objętość bryły otrzymanej z obrotu wskazanej figury wokół wskazanej osi: adaś: Oblicz objętość bryły otrzymanej z obrotu wskazanej figury wokół wskazanej osi: ox T={(x,y):0<=x<=^π₆, 0<=y<=tg2x} Bardzo proszę o rozwiązanie całego zadania krok po kroku.

Nienor:

	1
V=		π∫0π6 (tg2x)2 dx
	2

wynika → http://pl.wikipedia.org/wiki/Bry%C5%82a_obrotowa

Trivial: A skąd ta jedna druga?

Trivial: Zresztą po co pamiętać te wzory. Wystarczy znajomość całek wielokrotnych i wyprowadzenie zajmuje jedną linijkę. V = ∭_V dV = ∫₀^2π dφ*∫_a^bdx∫₀^f(x) rdr = π*∫_a^b f²(x)dx

adaś: Dobrze, wzór znam, ale co podstawiam za a i b a co za funkcję f(x).

Nienor: Bo się pyta o połowę takiej figury, tę co leży nad płaszczyzną OX. Wzór opisuje całość. Nie każdy zna całki wielokrotne (jak się je zna, to wychodzi to jakoś naturalnie i się zwykle o to nie pyta)

Trivial:

	π
No jak to, wszystko masz podane jak na tacy. a = 0, b =		, f(x) = tg2x.
	6

adaś: Teraz wszystko jasne, dziękuje za pomoc !

Trivial: 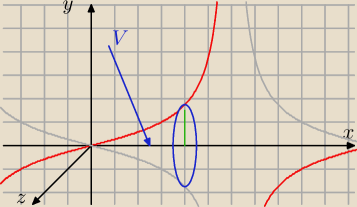Nienor, dlaczego o połowę? Ja widzę granice dla x, i y.

Trivial: Źle się wyraziłem. Widzę granicy dla figury, a nie bryły. Tak otrzymaną figurę potem obracamy dookoła osi Ox.

Nienor: haha, dobra nie ważne. Masz rację Trivial. Coś mi ten skrót myślowy nie wyszedł