Liniowa Ajtek: Mam sprawę do Was mądrych . Mianowicie, mam zadanie typu: Dla jakich wartości parpametru m funkcja f(x)=−3x+5−2m przecina oś OY poniżej punktu P(0;7). Nie chodzi mi o rozwiązanie, bo z tym sobie poradziłęm, tylko jak wytłumaczyc znak nierówności. Ja chłopakowi poeiwdziałem w ten sposób: Jeżeli funkcja jest malejąca, to musisz napisać znak przeciwny, czyli jak przecina poniżej to znak ">", jak powyżej to znak "<". Ktoś podpowie

fdsf: będzie −3x+5−2m ponieważ jest malejąca musimy zapisać w postaci −3x+5−2m<0

Ajtek: fdsf rozwiąż to i podaj odpowiedź . Mam 100% pewności że jest zła.

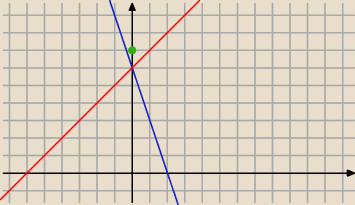
asdf: nie bardzo wiem co ma monotoniczność do rzeczy tutaj. 5−2m < 7 f(x) = −3x +6 h(x)= x + 6 P(0,7)

Piotr: sorry ale wg mnie to nie jest dobre. nie będzie wiedział o co chodzi tylko tak się "nauczy". to trzeba rozumieć. Ale z drugiej strony i tak będzie lepszy od całej reszty, która w ogóle nie będzie wiedziała o co chodzi. ja bym mu kazał narysować przykładowe f. liniowe malejące i rosnące i żeby sam doszedł do odpowiednich wniosków. Ale to tylko ja

Lorak: hm.. moim zdaniem wystarczy rozwiązać 5 − 2m < 7

asdf: niech P(x) = 7, czyli P(0)=7 f(x) = −3x + 5−2m, f(0) = 5 − 2m poniżej punktu, czyli, dla jakiego m funkcja f ma mnieszą wartość od P w punkcie x = 0: f(0) < P(0) ....

Ajtek: asdf f. jest malejąca. Rysunek jest okej. Tez w ten sposób kombinowałem tylko nie dałem f. rosnącej. Piotr, dlatego pytam. chce dać ta wiedzę Jemu, tylko nie wiem jak mam to powiedzieć, wytłumaczyc. asdf dał mi pewien pomysł.

Ajtek: Lorak dzięki . Za bardzo się wczułem w pierwszą lekcje i zapomniałem o podstawach

Bogdan: Po pierwsze − funkcja nie przecina osi OY, tylko wykres funkcji przecina tę oś. Wykres: y = −3x + 5 − 2m, a = −3, b = 5 − 2m Jeśli prosta y = ax + b przecina oś OY w punkcie (0, y₀), to y₀ = b Trzeba więc rozwiązać nierówność: 5 − 2m < 7 ⇒ m > −1

Ajtek: Witaj Bogdan . Wiem że funkcja nie przecina osi, tylko wykres tej funkcji. Pisałem to na szybko, nie dawało mi to spokoju. Twoje uwagi jak zawsze są cenne .