Ostrosłup Ewelinka: Zad. 1 Wysokość ostrosłupa prawidłowego trójkątnego jest równa 5 cm, a krawędź boczna ma 13 cm. Oblicz wysokość ściany bocznej tego ostrosłupa. Zad. 2 Mrówka przeszła po powierzchni sześcianu z wierzchołka A do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka A, przy czym była to droga najkrótsza z możliwych. Narysuj siatkę sześcianu, a następnie oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość √5 m (Już może być bez rysowania siatki) Proszę o pomoc! Dziękuję z góry

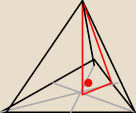
Janek191: z.1 H = 5 cm b = 13 cm a − długość boku trójkąta równobocznego h₁ − wysokość Δ równobocznego h₂ − wysokość ściany bocznej Mamy h₂² + ( 0,5 a)² = b² czyli h₂² + 0,25 a² = 169

	1		1
(		h1)2 + H2 = h22 czyli		h12 + H2 = h22
	3		9

	a√3		3
h1 =		⇒ h12 =		a2
	2		4

dlatego h₂² + 0,25 a² = 169

1		3		1
	*		a2 + 25 = h22 ⇒		a2 + 25 = h22 ⇒ 0,25 a2 + 75 = 3 h22 ⇒
9		4		12

⇒ 0,25 a² = 3 h₂² − 75 czyli h₂² + 3h₂² − 75 = 169 4 h₂² = 244 h₂² = 61 h₂ = √61 Odp. h₂ = √61 cm ===================

Janek191: z.2 x² = ( √5)² + ( 2 √5)² = 5 + 20 = 25 x = √25 = 5 Odp. 5 m ============

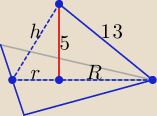
Bogdan: proponuję takie rozwiązanie:

	12
R = 2r, R = √132 − 52 = 12, r =		= 6, h = √52 + 62 = √61
	2

Ewelinka: Dziękuję bardzo